5.1 Introduction
In the previous chapter, practical applications of the Tone Clock were demonstrated, concluding that it can serve as a useful tool to embed twelve-tone techniques in the improvisational languages of contemporary jazz artists. In this chapter, I will discuss a compositional technique that also contains serial elements, yet with more obvious tonal references: Messiaen’s modes of limited transposition.
As well as composing an impressive oeuvre, Messiaen disseminated his theories and practices in a large number of publications, such as the seven volumes of the comprehensive Traité de rythme, de couleur, et d’ornithologie (1949-1992) and the earlier1 and more compact Technique de mon langage musical (1956), in which he explained his modes of limited transposition for the first time.
Organist and theorist Vincent Benitez (2008) explains that Messiaen’s modes of limited transposition, devised in 1929, originated from his improvisation classes with composer-organist Marcel Dupré, which implied the application of unconventional modalities as part of the Catholic liturgy. Benitez also claims a close relationship between Messiaen’s abilities as an improviser and the applications of the modes in his compositions, because in a number of passages he examined, “the harmonies lie comfortably in the hands, suggesting that they emerged from Messiaen’s improvisations” (Benitez 2008: 135).
The first time I became acquainted with Messiaen’s modes of limited transposition was in my days as a saxophone student, practicing Guy Lacour’s 28 Etudes pour saxophone sur les modes à transpositions limitées d'Olivier Messiaen (Lacour 1972). Lacour arranged the transpositions of all seven modes into comprehensive exercises that caught my interest by their mysterious sounds. However, presenting a book with technical exercises to enhance the dexterity of saxophone players, Lacour did not explain the theoretical or aesthetical context of these modes within the complex musical universe of Messiaen, nor its possible application to (jazz) improvisation.
In the context of this study, I will neither examine the role of the modes in Messiaen’s oeuvre, nor his practices as an improviser. My fascination with Messiaen’s modes concerns their options for (composing) improvisers to transcend conventional tonal practices. In section 1.4.4, I mentioned as my motivation for this study that I was unhappy with my writing and improvisations. Can operations with Messiaen’s modes satisfy my need for innovative harmonic issues as alternatives to my practices with the tonal system? Just like the twelve-tone related techniques in chapter 4, I consider the operations with Messiaen’s modes, discussed in this chapter as practical tools with the potential to help (composing) improvisers enriching their artistic palette. Since the focus in this study is mainly on the melodic and harmonic applications, other compositional techniques developed and discussed by Messiaen, such as his comprehensive approach to rhythm, will only receive limited attention.
The layout of this chapter is as follows. After an outline of Messiaen's basic theory in subchapter 5.2, subchapter 5.3 displays interval analyses of all modes followed by examples of basic mode embellishments. In subchapter 5.4, I discuss applications of Messiaen’s modes of limited transposition in the jazz practices of guitarist Nelson Veras, baritone saxophonist Bo van der Werf, tenor saxophonist Jasper Blom, and soprano saxophonist Steve Lacy. Instead of presenting a historic overview of jazz artists who applied Messiaen’s modes in their compositions and improvisations, for instance from guitarist Jim Hall’s composition “Two’s Blues” on the LP Concierto (1975), via drummer Bill Stewart’s compositions on the CD Telepathy (1997), to pianist Pablo Held’s improvisations such as in “Gray” on Sebastian Gille’s CD Anthem (2011), I decided to focus on the works of Veras, Van der Werf, Blom, and Lacy, because, in their compositions and improvisations, and in the relationships between them, they show a diversity of applications of all of Messiaen’s modes that are relevant in the context of this study.
Then, in subchapter 5.5, I will discuss a number of examples of my own applications of Messiaen’s modes. Questions that will be dealt with are: How do my works relate to Messiaen’s ideas and to the works discussed in subchapter 5.4, and how do they contribute to my research aim to investigate techniques helping (composing) improvisers to move beyond their usual tonal practices? Subchapter 5.6 contains a generative compendium of melodic patterns, meant to serve other musicians as a point of departure for creating their own variations. In subchapter 5.7, the operations with Messiaen’s musical techniques in this chapter will be evaluated in the context of my principal research question and the methods discussed in chapters 3 and 4.
ex 5.2.2.4
5.2.3 Third mode (M3)
Structure of M3
Messiaen divides his third mode of limited transposition (M3) into three symmetrical groups of four notes (each). It has four possible transpositions. Messiaen refers to this mode as “the chord of the augmented fifth” (Messiaen 1956: 60). M1 (the whole-tone scale) is embedded in this nine-tone scale.
ex 5.2.4.3
In the following example, the operations “skip 2 notes”, “skip 6 notes”, and “skip 4 notes” work well to illustrate the characteristic sound of M4. They all result in two segments containing dyads with dissimilar intervals. In the first and second lines they are ordered a–a–a–b, in the third line they are ordered a–a–b–a.
ex 5.2.5.4
5.2.6 Sixth mode (M6)
Structure of M6
According to Messiaen, his sixth mode is formed with two segments of five notes. Each group contains two major seconds followed by two minor seconds.
ex 5.2.7.2
Embellishments of M7
Operation “skip 4 notes” results in a succession of similar intervals of augmented fourths within two segments at the distance of an augmented fourth.
ex 5.2.2
In order to make the embellishments in the following sections sound less predictable, I will randomly add variations to them, by alternating the ascending and descending directions of the lines and the dyads.
ex 5.2.1.2
Embellishments of M1
The following examples display the “skip 1 note”, “skip 2 notes”, “skip 3 notes”, and “skip 4 notes” operations on all (accentuated) degrees of the basic mode. They result in successions of similar intervals, respectively major thirds, augmented fourths, augmented fifths, and minor sevenths. In bars 1–2, and in bars 7–8, all intervals are played in ascending direction. In bars 3–4, and 5–6, the intervals are played in alternating ascending and descending directions. The successions of six similar intervals emphasize the characteristic symmetry of the whole-tone scale and its tonal color of the augmented chord (see section 5.6.1).
ex 5.2.3.1
Interval analysis reveals that two ways of grouping the segments are possible. The first line reflects Messiaen’s division shown above, displaying three 2+1+1 tetrachords, with every next tetrachord starting on the last note of the preceding one. The second line shows that, without repeating the root note, it can also be considered as a sequence of three 2+1 trichords at distances of major third intervals.
ex 5.2.4.2
Embellishments of M4
Operation “skip 3 notes” perfectly illustrates the symmetry of CM4: two symmetrical segments at an augmented fourth distance, both containing a succession of dyads with the same augmented fourth intervals.
ex 5.2.6.2
Embellishments of M6
The next succession of dyads with similar intervals of augmented fourths inside two segments at an augmented fourth distance results from operation “skip 3 notes”.
ex 5.2.6.4
5.2.7 Seventh mode (M7)
Structure of M7
With ten pitches, the seventh mode contains the largest number of pitches of all modes. It is only two pitches away from being a chromatic scale. According to Messiaen it is formed with two groups of six notes. Each group displays the intervallic structure of three minor seconds, followed by one major second and another minor second.
ex 5.2.7.4
To summarize the exposition of Messiaen’s seven modes, both the interval analyses and the embellishments of the modes illustrate Messiaen’s notion of the “charm of impossibilities” (Messiaen 1956: 58). With this term, he indicates the “strange charm” of the modes due to their limited transpositional possibilities. However, this does not mean that the sound of the modes becomes more interesting when the amount of their transpositions is smaller. Certainly, M1 (two transpositions), M2 (three transpositions), and M3 (four transpositions) have strong characteristics. However, in my opinion, the same goes for (the embellishments of) M4, M5, and M6, which contrasts with Messiaen’s statement that they are “transposable six times, and presenting less interest, for the very reason of their too great number of transpositions” (Messiaen 1956: 58). In the case of M7, I consider the large amount of pitches, rather than the numerous possible transpositions, as the main reason for being less interesting.
Based on my musical experiments and experience, I maintain that my examples of mode embellishments manage to create a form of “strange charm” even to the less interesting modes; besides, they also enhance the charm of the less transposable ones. Therefore, in my predominantly melodic approach to Messiaen’s modes, embellishment techniques are as important as the numbers of possible transpositions.
The interval analyses I have added as an alternative to Messiaen’s expositions of the modes are meant to mark the segments they are formed with more precisely. Thus, the symmetry of their segments, responsible for their characteristic tonal ambiguities, is illustrated more clearly, helping the musician to either emphasize the various tonalities or to leave them aside. After all, according to Messiaen, his modes are “at once in the atmosphere of several tonalities, without polytonality, the composer being free to give predominance to one of the tonalities or to leave the tonal impression unsettled” (Messiaen 1956: 58).
The following subchapter discusses applications of Messiaen’s modes by four (composing) improvisers introduced in subchapter 5.1. How do Veras, Van der Werf, Blom, and Lacy use the modes, and how do they treat the tonal ambiguities? Rather than present a kind of historic overview, I have selected their works because they show melodic applications of one or a limited number of modes in a way that connects to the predominantly melodic approach to improvisation that is the subject of this study. Moreover, taken together, the following four examples show applications of all seven modes.
5.2.1 First mode (M1)
Structure of M1
The first mode of limited transposition (M1) is formed with six groups of two notes. Messiaen explains that M1 has two transpositions. In the following example, its basic form starting on the note c, is called the first transposition. The second is its transpositionup a minor second. The next transpositions are irrelevant because they would contain the same notes as the first and the second transposition.
ex 5.2.1.3
5.2.2 Second mode (M2)
Structure of M2
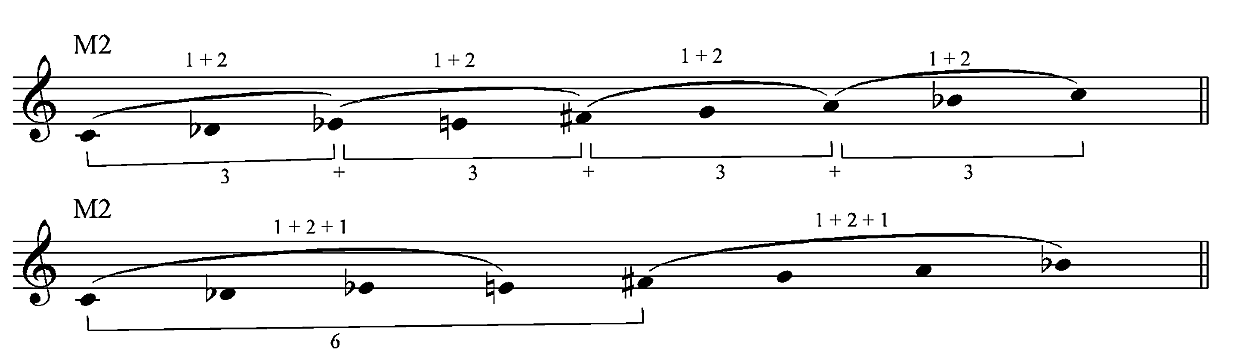
Messiaen’s second mode of limited transposition (M2) has three transpositions. It is formed with four symmetrical groups of three notes (each). Thus, M2 displays four trichords, themselves divided into two intervals: a minor second and a major second.
ex 5.2.2.3
Next, the operations “skip 2 notes”, “skip 4 notes”, and “skip 6 notes” result in segments containing dyads with dissimilar intervals: a perfect fourth (5) and a major third (4), a perfect fifth (7) and a minor sixth (8), and a minor seventh (10) and a major seventh (11). Because of these dissimilar intervals and their irregular directions, the following mode embellishments could sound less predictable than the ones in the example above.
ex 5.2.3.3
In the following lines, the operations “skip 3 notes”, “skip 4 notes”, “skip 6 notes”, and "skip 7 notes”, result in segments containing combinations of dissimilar intervals. Augmented and perfect fourths, perfect and diminished fifths, minor sevenths and major sixths, and major and minor sevenths, appear in different orderings: a–b–b in bars 1 and 3; a–b–a in bars 2 and 4. The combination of these larger intervals with their specific orderings highlights the interesting structure of this mode that, constructed of three symmetric segments, includes the minor and major thirds as well as the minor and major sevenths on the “root notes” of the parallel segments.
ex 5.2.4.1
Interval analysis of this mode without repetition of the initial note reveals two tetrachords with the similar intervallic construction 1+1+3, two minor seconds and a minor third, at the distance of an augmented fourth.
ex 5.2.5.1
The following interval analysis of this mode without the initial note repeated reveals two 1+4 trichords at the distance of an augmented fourth.
ex 5.2.5.3
Operations “skip 1 note” and “skip 2 notes” result in the interval groupings of perfect fourths and major seconds, and major seventh and minor sixths, both in the order a-a-b. The third line shows combinations of perfect fifths and minor sevenths in the order a-b-a.
ex 5.2.6.1
Interval analysis of the sixth mode without repetition of the initial note displays two 2+2+1 tetrachords at the distance of an augmented fourth (6). In other words, Messiaen’s mode M6 displays the first tetrachords of the C and the F♯ major scales.
ex 5.2.7.3
The following example shows how operation “skip 2 notes” results into two segments containing successions of dyads with minor and major thirds in the order a-b-b-b-a. In the second bar “skip 7 notes” creates successions of major sixths and minor sevenths in the order a-b-a-b-a.
ex 5.2.1
The exposition of his “own modes of limited transposition” (Messiaen 1992 VII: 50) is only one of Messiaen’s compositional techniques. Their potential for application by (composing) improvisers will become evident from the practical examples discussed in this chapter. Other techniques such as extended rhythms and operations with “non-retrogradable rhythms” (rhythmic palindromes: rhythms that, played from right to left, sound the same as played from left to right) will be less apparent. Looking back to the concepts of “playing outside the chords” and “creating intended harmonic vagueness,” introduced as potential techniques to develop the improviser’s personal sound in chapters 1 and 2 of this study, the important question is how these operations with Messiaen’s modes can enhance the practices of (composing) improvisers.
The arrangement of this subchapter is as follows. Sections 5.2.1 – 5.2.7 are meant to expose the structures of Messiaen’s modes. Each section displays the basic mode followed by an analysis of its intervallic and segmental structure. This is followed by examples of so-called “mode embellishments” which I define here as scale variations. Dividing the scales into dyads with intervals that can be gradually increased (starting with thirds, then fourths, fifths, etcetera), could be applied effectively to study the individual colors of Messiaen’s modes. I connect each degree of the mode to the one that is a fixed number of steps higher or lower. Put in its simplest form, I call these embellishments “skip 1 note”, “skip 2 notes”, “skip 3 notes”, etcetera.
The following example illustrates the application of the “skip 1 note” embellishment to CM3, resulting in three segments at a major third (4) distance, each containing a combination of a minor third (3), a major second (2), and again a minor third (3). Regarding the notation, the intervals within the dyads are written above the staff, unless all intervals are similar. In the latter case, they are omitted. The intervals between the segments are written under the staff. The degrees of the basic modes are always accentuated.
ex 5.2.1.1
M1 can be identified as the whole tone scale. It is also embedded in the modes M3 and M6 (see 5.2.3 and 5.2.6).
Interval analysis shows that there are two ways to divide M1 into two symmetrical segments. Instead of Messiaen’s six groups of two notes, two groups of four notes are marked in the first line, still matching his principle of “the last note of a group always being common with the first of the following group” (Messiaen 1956: 58). The second line displays M1 as two separate trichords, arranged at the distance of an augmented fourth, without repetition of the root note c.
ex 5.2.2.1
Among jazz improvisers, Messiaen’s second mode is widely known as the octatonic (eight-tone) scale, or as the diminished scale ordered in a succession of minor and major seconds (the so-called “half-tone–whole-tone” ordering). In the first line of the following example, interval analysis reveals four overlapping 1+2 trichords, steered by intervals of minor thirds, with every next group starting on the last note of the preceding one. In the second line the eight-tone scale is divided into two segments of 1+2+1 tetrachords at a tritone distance. Both lines clearly express the symmetry of this mode.
ex 5.2.3.2
Embellishments of M3
M3 allows the improviser a large variety of scale embellishments. The operations “skip 2 notes” and “skip 5 notes” result in three segments at a major third (4) distance, each containing three dyads with similar intervals: major thirds, and their inversions, minor sixths.
ex 5.2.3.4
5.2.4 Fourth mode (M4)
Structure of M4
Messiaen relates his modes M4, M5, M6 and M7 to the interval of the augmented fourth: “These modes are transposable six times, like the interval of the augmented fourth” (Messiaen 1956: 61). Each of these four modes can be divided into two symmetrical groups, an augmented fourth interval apart. Messiaen divides M4 into two groups of five notes as follows.
ex 5.2.5.2
Embellishments of M5
Operation “skip 2 notes” in the following example demonstrates the symmetry of M5. Just as in section 5.2.4 two symmetrical segments appear at an augmented fourth distance, both containing a succession of dyads with the same intervals.
ex 5.2.7.1
Interval analysis of the mode without repetition of the initial note displays two groups of five notes at a distance of an augmented fourth interval. Each of the two groups consists of three minor seconds and one major second.
ex 5.2.4.4
5.2.5 Fifth mode (M5)
Structure of M5
The fifth mode of limited transposition (M5) is the same as the fourth, but with the third and the seventh note omitted. According to Messiaen, it is formed with two groups of four notes as follows.
ex 5.2.6.3
The application of operation ”skip 1 note” on CM6 creates the most complicated interval collection so far: both segments, arranged at the distance of an augmented fourth (6), in the first line of the following example contain dyads with intervals of a major third, two minor thirds, and a major second in the order a-b-c-b. Operation “skip 2 notes” executed in the second line creates two segments containing two perfect fourths and two major thirds in the order a-b-b-a. By manipulating the directions of the intervals, both lines manage to obscure the bare symmetric structure of CM6.
5.2 Messiaen’s seven modes of limited transposition
Throughout his career as a composer and educator, Messiaen has explained his modes of limited transposition in a number of publications, the first being Technique de mon langage musical (1956). Meant for the students who wanted to get acquainted with his works, the “little theory” is accompanied by a second volume with musical examples quoted from his own works. In chapter XVI Messiaen exposes the “mechanism” of his seven modes of limited transposition that “can be used melodically, and especially harmonically, melody and harmonies never leaving the notes of the mode” (Satterfield in Messiaen 1956: 58).
In volume VII of his impressive Traité de rythme, de couleur, et d’ornithologie (1992) Messiaen provides more detailed information on the structures and applications of modes 2, 3, 4, and 6. He explains that his modes of limited transposition have nothing to do with tonalities, neither with rows, nor with (his detailed expositions of) Chinese, Hindu, Greek, and church modes, claiming that “the chords that can be formed with the modes have to be thought and read modally, and not following the rules of classical harmony” (Messiaen 1992: 50, my translation). Rather than in terms of tonic and dominant, or serial principles, he defines them as “colors, harmonic colors. Every mode […] has its particular color, due to that actual impression of a closed door, or a closed circuit, and also to the different combinations of sounds which cause its limited number of transpositions” (Messiaen 1992: 51, my translation).
How does the concept of limited transposition work? In contrast with conventional diatonic scales and modes, occurring in twelve possible transpositions, the options of transposing Messiaen’s modes are restricted, because beyond a certain number of transpositions the same notes will sound again. For instance, as shown in the following example, taking CM2 (“M2” refers to the second mode, while the “C” indicates the first note of the mode) with its three possible transpositions (bars 1–3), the fourth transposition (bar 4) displays exactly the same notes as the first, while the fifth (bar 5) will give exactly the same notes as the second (bar 2).
ex 5.2.2.2
Embellishments of M2
Both the symmetry of M2 and its tonal color of the diminished chord are illustrated in the following lines. All of the operations, “skip 1 note”, “skip 3 notes”, and “skip 5 notes”, divide the mode into four symmetric segments at a minor third distance. Each segment contains two dyads with similar intervals: minor thirds, augmented fourths, and major sixths. In order to avoid a predictable sound, I randomly modified the directions of the dyads and the lines.
ex 5.3.2.4
“Calcutta” (Bo van der Werf) – alto saxophone solo fragment
The next example shows the first half of Van der Werf’s baritone saxophone solo, played on the second solo form. The accompanying chords are the same as in the first solo form, but now the chords are played twice as fast, and strongly punctuated. In contrast with the predominant chord-scale approach in the alto solo, Van der Werf plays a loose application of F♯M2 as an overall superimposition on the complex rhythmic and harmonic structure accompanying his solo.
The encircled passages in the transcription mark the fragments containing F♯M2 patterns with zero or few notes added to the basic mode. These additions are either chromatic passing tones, such as the notes d and b in bar 3, or notes added intentionally such as the note d in bar 7, g♯ in bar 17, and b in bars 18 and 19.
The brackets above selected groups of notes mark the tonal colors appearing alongside the basic F♯M2 mode. These excursions outside the mode are the result of Van der Werf sparsely adding neighboring notes. Because of this, the notes within the brackets sometimes overlap the encircled fragments.
ex 5.3.3.1
“Let’s Give This Tree A Little Friend” (Jasper Blom) – mini score first section
Further on, the solo section of Blom’s composition is introduced by a “break” played in unison and octaves by the saxophone section. This line is a “skip 1 note” embellishment of A♭M3 (see ex 5.2.1). The final chord E♭maj7#5 (add#9) is built on the fifth degree of A♭M3.
example 5.3.3.5
“Let’s Give This Tree A Little Friend” (Jasper Blom) – saxophones repeating the main theme
Evaluation
Both in the composed and in the improvised parts, “Let’s Give This Tree A Little Friend” demonstrates how the ambiguous tonalities in Messiaen’s third mode can be used to create adventurous musical content. The construction of the composed parts is kept relatively simple in comparison to Van der Werf’s “Calcutta”, and the operations with M3 and M6 are quite basic. As an addition to Messiaen’s compositional techniques applied by Van der Werf, Blom demonstrates the creating of parallel harmonies, by stacking parallel successions of notes along the order of the modes. In his first tenor saxophone solo he shows obvious operations with M3, highlighting the mode’s characteristic ambiguous harmonic content. Altogether he manages to create an unconventional musical space incorporating a clear relation between the composed and the improvised parts of his piece.
ex 5.3.1.1.3 Nelson Veras third example
After these technical demonstrations, Veras discusses his aesthetic approach to the Messiaen modes, which is principally melody-oriented. As he explains during the workshop: “I like the sound of these modes melodically. I like them harmonically too but I like just the melodies that can appear. … Actually I avoid the symmetry of it. I try to not play, say, all the time like…” plays the following two sequences.
ex 5.3.1.2.1 Nelson Veras sixth example
Then, as shown in bars 1–3 of the next example, he plays the same mode, but now starting on the last note, to create a Bm tonality. The lines in bars 4–5 and in bars 6–10 show embellishments of Bm. Despite their increasing complexity, Veras almost never leaves the notes of the mode. The note d♯ in bar 10 is the only exception.
ex 5.3.3.2
“Let’s Give This Tree A Little Friend” (Jasper Blom) – break by saxophones
After this break, the saxophone quartet repeats the first line of the main melody, as a “send-off” to Blom’s unaccompanied solo. The line is now arranged in a parallel harmony of five stacked layers of CM3, each starting on different positions of the mode2. These positions are marked above the brackets. They refer to the three implied tonalities of C, E, and A♭ within CM3. Only in the alto saxophone and first tenor saxophone parts do the lines start on the root notes of these tonalities. In all other parts the lines are marked after the root notes that are closest to the first note of the line.
ex 5.3.3.4
“Let’s Give This Tree A Little Friend” (Jasper Blom) – tenor saxophone solo first fragment
After this solo the saxophones repeat the main theme, again arranged in a five-part parallel harmony. In bars 1–3 all lines are again samples of CM3, starting from different positions in the mode. This also goes for the descending line in bars 6–7. The descending line in bars 4–5, however, breaks the overall unity of CM3. By playing EM3 (encircled) the baritone saxophone persists, but the parts of the remaining four saxophones play parallel harmonies with AM3, starting from different positions in the mode.
5.3.4. Steve Lacy “Prayer”
In his composition “Prayer,” soprano saxophonist and composer Steve Lacy combines transpositions of M3 and M5 in an arrangement for sextet, plus two vocalists reciting a poem written by Galway Kinnell, on the CD Anthem (1990).
In bars 1–4 the three horns play the triads Db, Eb, and F#11(omit5). Together the notes in these bars form the mode DbM3(add b♭). The two-bar ostinato by piano and bass can be considered an incomplete representation of DbM3 (add b♭). Its missing notes f, g, a, and b, are played by the horns.
In bars 5–8 a two-part harmony line by the saxophones and the two vocalists exposes the main melody using notes from mode CM5(add b♭). The trombone now plays a contrapuntal line in which a chromatic succession between the notes g♭ and b leads to bar 8 where he plays the first half of CM5.
In bars 9–12 the vocalists continue their melody with CM5 in alternating orders and directions, emphasizing the symmetry of the melody line in which the second half is the inversion of the first line transposed up an octave. The soprano saxophone and the trombone play contrapuntal lines that again represent DbM3(add b♭), now with the addition of the note g♭.
ex 5.3.4.2 "Prayer" (Steve Lacy - soprano sax solo fragment)
Evaluation
Compared to the comprehensive compositions by Van der Werf (2006) and Blom (2014), Lacy creates a convincing result with limited means, and with a small line-up. By means of the many repetitions of the mode, he evokes an almost spiritual atmosphere. Lacy’s dividing of the mode between the horns and the rhythm section, thereby considering the latter as the complement of the incomplete D♭M3(add b♭) in the horn section, is an interesting compositional operation. Even more convincing are his contrapuntal lines, particularly the trombone line in bars 9–12, displaying a contrast with the straightforward mode pattern in the soprano saxophone part. Further on, the first fragment of Lacy’s improvisation shows a deliberate selection of notes from D♭M3, creating an unconventional superimposition on the D♭-pedal point played by the rhythm section.
ex 5.3.1.1.2 Nelson Veras second example
In bars 1–2 of the next example, Veras plays the embedded b whole tone scale. BM3 matches here with BM1 as discussed in sections 5.2.1 and 5.2.3. Finally, in bars 3–4 he plays a sequence of embedded minor triads, starting with F#m and ending on Bm, the root of BM3. With this example, he shows that minor triads can be built both on the roots of the three implied tonal centers, and on the preceding notes in the mode. The C minor chord in bar 4 is marked with an asterisk because it is foreign to mode BM3.
ex 5.3.1.1.4 Nelson Veras fourth example
Veras continues, ”I try just to see where it takes me plays bars 1–5 of the following examples and what kind of colors I can find plays bars 6–22.” There is a noticeable difference between these two fragments. In bars 1–5 Veras strictly keeps to the notes in the mode. Only in the last bar does he add the note c, which is foreign to the mode, evoking the sound of Cm. Then, in bars 6–22 he continues playing the note c, and combines this with two other notes that are not in the mode: e and a♭. The notes that sound outside the mode are marked by an asterisk. Together these notes form the augmented triad c –e–g♯, sounding a minor second above the basic triad b–e♭–g of the mode. It could be considered as a tritone substitute of its F# dominant-seventh chord.
Furthermore, in bars 6–22 five three-voice harmonies appear. Two of these, in bars 12 and 16, can be identified as B diminished and Bm triads. The others are the incomplete F#maj (omit5) /A# chord in bar 8, and two cluster chords in bars 7 and 10 that can both be regarded as first rotations of 1+5 trichords.
ex 5.3.1.1.5 Nelson Veras fifth example
With his application of BM3 that combines an intelligent usage of the mode with a deeply embodied knowledge of functional harmony, Veras manages to create unconventional melodic lines that evoke an intended harmonic vagueness. Admittedly, he occasionally leaves the mode. As such, he seems to act in conflict with Messiaen’s intentions as discussed in subchapter 5.2, of “never leaving the notes of the mode.” However, I agree with Veras that these “false” notes are acceptable both from an aesthetic perspective (“they sound good in the line”) as well as from the perspective of the jazz improviser: risk-taking is an important part of the improvisational practice. Thus, Veras’ approach convincingly proves the potential of M3 in the context of the subject of my research.
5.3.1.2 M6
Veras’ approach in subsection 5.3.1.1 is also obvious in his operations with M6 as shown in the following examples. First, he demonstrates his tactic named “everything you do on this one, you can do a raised four above.” After exposing the basic mode CM6 he illustrates its characteristic sound, playing a sequence of tetrachords at distances of an augmented fourth (6).
ex 5.3.1.3.2 Nelson Veras tenth example
In the next example Veras introduces the G7b9 chord, as a parallel to the Db tonality in the example above. The resulting line shows an advanced blending of the tonalities D♭, G, and Bm. The D♭ chord appears both as a major seventh and a dominant seventh chord. With F minor and Bm considered as the third degrees of D♭maj7 and Gmaj7, the following line strictly covers these two tonalities appearing at a tritone distance in CM4.
ex 5.3.2.1
The next example shows the bass melodies in sections A and B. They are different from the solo form above, and arranged in a non-retrogradable rhythm: section B contains the retrograde of the rhythmic structure of section A. Both sections are identical, except the encircled notes. The bass line as a whole contains seven fragments in which seven Messiaen modes can be identified, reflecting a symmetrical structure in this part. C#M4 and GM4 contain the same notes, just like F#M7 and CM7. The first two modes of A and the last two modes of B do not match, but the third and fourth of A and the first and second of B do.
[A] C♯M4 – C♯M7 – C♯M4 – GM4 [B] GM4 (continued) – GM4 – F♯M7 – CM7
ex 5.3.2.2 “Calcutta” (Bo van der Werf) - bass line
The melody lines in section A and B contain fragments of chromatic scales. Although these fragments imply transpositions of all of Messiaen modes, it does not make sense to mark them individually. Therefore, I rather consider them as incomplete chromatic scales. In the following example I have subdivided section A into parts of roughly two bars, each displaying distinct fragments. The range between the lowest and the highest note of each fragment is marked above the brackets. Listing the intervals between the lowest and the highest notes displays another symmetric structure. From the first to the last line in section A, the intervals are getting larger. From the first to the last line of section B, the intervals are getting smaller, in both sections by groupings of two, one, and two lines. The axis of the symmetry is between bars 10 and 11.
Résumé
So far, the analyses in this subchapter have disclosed various applications of M2, M3, M4, M5, and M6. M6 was announced quite often, but only sparsely applied. Veras showed a useful approach to M6 in his improvisation examples, Blom applied it in his contrapuntal lines, and in Van der Werf’s piece it got sporadic applications both in the composition and in the alto saxophone solo. The most frequently applied was M3. Veras and Blom referred to its implied minor, diminished, major, and augmented triads and seventh chords. The aesthetic qualities of M4, and particularly M5, were emphasized by their repetitive applications in Lacy’s piece. M7 could be found in Van der Werf’s composed bass line as a result of notes added to M4.
However different the compositions and solos, they all illustrate the potential of Messiaen’s modes to be applied as advanced operations for (composing) improvisers creating less conventional musical spaces. Yet, it should be noted that, in the strict sense, the addition of notes outside the actual modes, found in all pieces analyzed here, does not match Messiaen’s original aim of “never leaving the notes of the modes.” Although I advise my students to avoid the addition of “foreign” notes as much as possible (see section 5.3.2), I simply cannot disapprove of these additions in the practices of (composing) improvisers applying the modes to create fresh and meaningful musical content, combining the modes explicitly or intuitively with their conventional improvisational languages.
Unfortunately, operations with basic or advanced mode embellishments, highlighting the splendor of the modes, are rare in the music analyzed so far. Only the operation “skip 1 note” could be identified in Blom’s saxophone section’s riff accompanying his solo. There, Blom is also the only one creating parallel harmonies with the modes.
In the next subchapter I will display my applications of mode embellishments and parallel harmonies, as well as a more comprehensive application of Messiaen’s sixth mode in some of my own compositions and improvisations.
Messiaen would have probably disliked the way jazz musicians run off with the contrived applications of his modes. In the examples so far, they are mainly commended for their ambiguous tonal colors, facilitating (composing) improvisers to connect them freely to various environments. He may even have denounced these connections as they contain the possible danger of “pan-tonality”, an interpretation of twelve-tone music in which, instead of all twelve pitches, all keys are equally important. I dare to counter this possible objection by quoting John Satterfield’s words in his “Introduction to the English Translation” of Messiaen’s Technique de mon langage musical: “The cataloguing and explanation of methods of building tonal structures may strike a creative response in a student or mature composer” (Satterfield in Messiaen 1956: 3). I consider the actual interventions with Messiaen’s modes as typical responses by creative jazz artists, founded on their traditions and broadening their artistic palette by adapting elements from surrounding musical worlds. This reflects my view of jazz music, expressed earlier in subchapter 1.2, acting as a guesthouse in which elements from other musical worlds are welcomed.
5.3 Applications of Messiaen’s modes in jazz
5.3.1 Master Class by Nelson Veras
An interesting blend of intuitive and well-informed applications of Messiaen's modes M3, M6, and M4 was demonstrated during a master class by Brazilian guitarist Nelson Veras at the Conservatory of Amsterdam on November 27, 2009. Veras strikes me as a creative improviser who, as he mentioned during his master class “is constantly looking for new ways to surprise himself.” The following sections examine a number of the lines he played, instantaneously responding to the questions by students attending this master class.
5.3.1.1 M3
Veras first plays BM3, Messiaen’s third mode starting from the root note b. In bars 1–3 of the example below he plays a succession of intervals of fifths and augmented fourths3, resulting from the operation “skip 4 notes” (see section 5.2.3), and ends with a conventionally arpeggiated Bm7 chord. Next, in bars 4–6, he illustrates the ambiguous tonal color of this mode by firstly extending the Bm7 chord before changing it into a B major triad at the end. Both tonal colors are implied in BM3 (see sections 5.2.3 and 5.6.3).
ex 5.3.1.1.1 Nelson Veras first example
In the following example Veras demonstrates how M3 can be considered as a sequence of three parallel tonal centers at distances of a major third. Due to this partition of the mode he explains that, without leaving the notes of the mode, “everything you do, you can do a major third above or below.”
In bars 1–2 he plays the three implied minor seventh chords Bm7, Ebm7, and Gm7. Bars 3–6 display symmetrical four-note patterns (2+2+1 tetrachords) at major third distances in alternating directions. In bars 3–4 interval analyses reveal a sequence of six 2+2+1 tetrachords, and in bars 3–6 a sequence of six 2+2+5 tetrachords. In bar 7 he plays a sequence of major seventh chords. All pitches in the examples below belong to mode BM3.
ex 5.3.1.2.2 Nelson Veras seventh example
Taking the note b as a pivot and building a B minor tonality on it, Veras inventively solves the “problem” of the two separate fragments from the tonalities of C and F# by merging them into one scale with a B minor tonal color.
5.3.1.3 M4
In the following examples, Veras demonstrates his operations with M4. After his exposition of CM4, he plays the mode up and down in bars 1–2. By stretching the notes b in bar 1, and g♯ in bar 2, he suggests the presence of the harmonic dominant on the fifth, sounding as the characteristic ending of the C major or minor harmonic scale: g–g♯–b–c. The fragment of the mode he plays in bars 3–5 continues to illustrate this tonal reference inside M4: the dominant-seventh chord with tension notes b9 and #11. It is resolving to the note c because since the minor or major third is lacking, it is not possible to create a conventional C chord. The notes under the bracket represent the scale of g mixolydian with passing notes between the root and the seventh and between the fourth and fifth degrees of the chord.
ex 5.3.1.3.1 Nelson Veras eighth example
Veras played the following lines to highlight the chords that are implied in CM4 as a kind of compensation for the “missing” C chord. In the first bar it is D♭maj7, and in bars 3–7 it is Bm. Bar 2 contains the root, the second, and the major seventh, representing a (very) incomplete C chord.
ex 5.3.1.3.3 Nelson Veras eleventh example
Evaluation
Veras offers instructive practical examples of improvising with M3, M6, and M4. He clearly shows their tonal ambiguities by concentrating on diatonic structures embedded in the modes as well as by picking various pivot notes as temporal tonal centers in order to simulate harmonic cadences. With his emphatic melodic approach of the modes, he convincingly demonstrates how he profits from their “soft guidance” to arrive at surprising tonal colors. I consider his sparse additions of “foreign” notes to the actual modes, resulting from his intuitive approach to improvisation, as acceptable operations from an aesthetic point of view, for instance in order to make lines sound less predictable, or to avoid the obvious symmetry of the mode. Thus, his applications of Messiaen’s modes M3, M6, and M4 show their potential to help (composing) improvisers move beyond the obsolete tracks of conventional harmony. Conversely, objections could be raised against the fact that his lines, however instructive and useful they are, only show one side of the coin. Freely scattering his applications of the actual modes, he does not limit them to any context of a composition or a set of chord changes. This particular aspect, the use of Messiaen’s modes in jazz compositions and the interactions of the improvisations with the composed material, will be addressed in section 5.3.2.
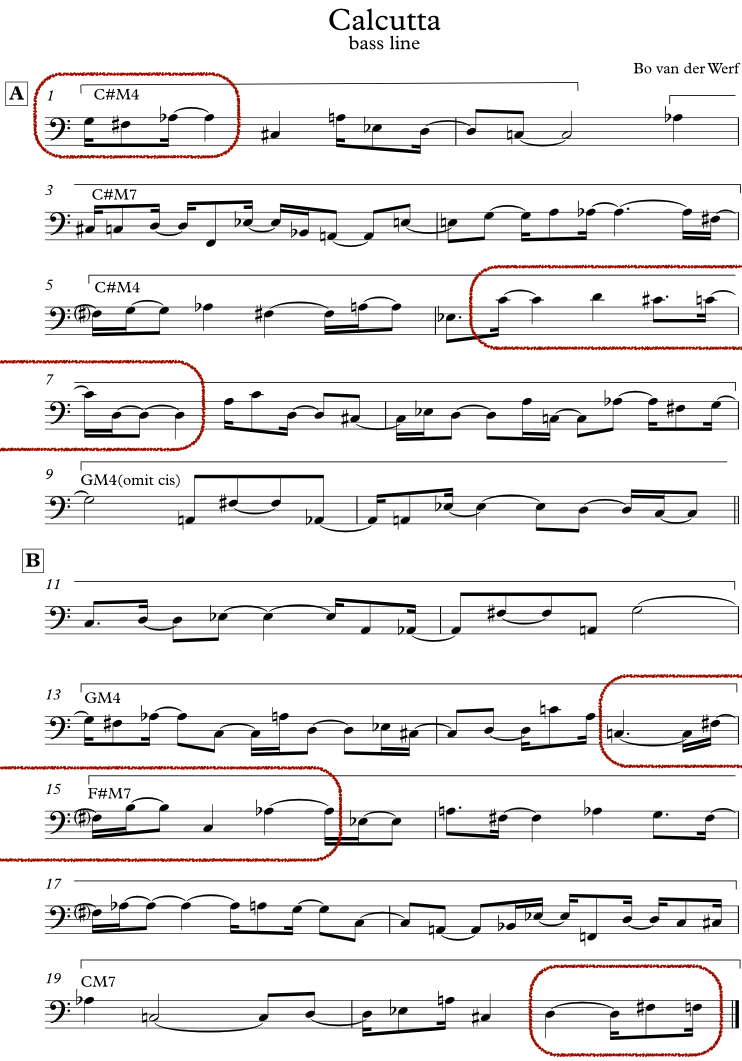
5.3.2 “Calcutta” (Bo van der Werf)
Baritone saxophonist and composer Bo van der Werf is widely known for his use of Messiaen’s compositional techniques in his writings for the ensemble Octurn, and in his improvisations. A recording of his piece “Calcutta” on the CD 21 emanations (2006) shows examples of multiple applications.
This section will first discuss the harmonic structure of "Calcutta" in relation to Van der Werf’s intended applications of Messiaen’s modes M2 and M6. Next, the contrapuntal bass and melody lines will be analyzed in relation to these modes. Finally, fragments of the alto saxophone and Van der Werf’s own solo on the baritone saxophone will be investigated.
“Calcutta” is based on the following rhythmic structure that contains two “non-retrogradable rhythms.” Messiaen coined this term for rhythmic palindromes: rhythmic sequences that, repeated in reverse order, sound the same. These are the non-retrogradable sequences in “Calcutta”:
a–b: 7/8 – 3/4 – 7/8 – 2/4 – 2/4 – 7/8 – 3/4 – 7/8
c–d: 3/4 – 7/8 – 3/4 – 7/8 – 3/4
The following example shows the first solo form, underlying the solos by the alto saxophonist and the guitarist. The upper staff exposes the tetra-chords that are continued throughout the tune, with the associated chord symbols written above them. The lower staff displays the bass notes of these chords with, written above them, Van der Werf's chord symbols or Messiaen modes M2 and M6. Van der Werf indicates that it is up to the soloist which of the lines to pick, but that his principal reference should be the succession of tetrachords notated in the upper staff and their relation to the bass notes.
In bars 3, 4, 6, 15, 18, 20, 21, 24, and 26 all pitches can be identified as members of various transpositions of M2. Bars 12, 20, and 22 contain one note that is not in the transpositions of the present M2: the fourth note from the root (add 11). In bars 7, 16 and 17 all pitches belong to various transpositions of M6.
ex 5.3.2.3 “Calcutta” (Bo van der Werf) - melody
The next example shows the transcription of the first half of the alto saxophone solo by Guillaume Orti over the first solo form as shown in example 5.3.2.1.
As noticed before, the solos can be based on both distinct accompanying lines in solo section A, but the principal reference should be the succession of tetrachords in the upper staff and their relation to the bass notes (example 5.3.2.1). Analysis of section A above confirmed a close connection between the pitches in the tetrachords and the transpositions of M2 and M6 indicated above the lower staff. In most cases, all notes belong to the actual mode, while only in a few cases are other notes added. How does Orti’s solo respond to the demands and the actual structure of this solo section?
The thirteen encircled passages show solo fragments in which the notes can be connected to an actual transposition of M2 or M6. Of the nine passages that contain transpositions of M2, seven match Van der Werf's suggestion written in the lower staff (example 5.3.2.1). These passages are marked with an asterisk. Four passages contain transpositions of M6, of which only one, marked with the asterisk in bar 16, matches the composer’s suggestion. The remaining bars contain melodic ornamentations of the chords written above them. In bars with the chords written in normal format, all notes fit in the actual chord. In bars with the chords written in cue notes, one or more notes sound outside the written chords.
Thus, in connection to Van der Werf’s arrangement of the solo section, Orti’s solo contains a mix of Messiaen’s modes and conventional chord ornamentations, both elements displaying variable grades of discipline. Just like Veras, both Van der Werf in his composed part, and Orti in his solo, take the freedom to occasionally leave Messiaen’s modes. Orti applies the same principle to the stated chord symbols, which creates a sound as if he is slightly playing outside the chords.
The operations above connect well to the usual practice of the jazz artist, whose principal goal is to instantly create musical lines that are meaningful in the context of their actual musical environment. Just like tonal ornamentations – tonal, and non-tonal superimpositions on conventional chord changes – these creative applications of Messiaen’s modes appear to be a useful tool, helping (composing) improvisers to broaden their artistic horizon.
ex 5.3.2.5
“Calcutta” (Bo van der Werf) – baritone sax solo fragment
Evaluation
“Calcutta” is a complex piece in which a variety of Messiaen’s techniques can be found, both in the composed and improvised parts. In his accompanying text “About ‘CALCUTTA’”, Van der Werf explains that the piece is based on two modes, M2 and M6, “but the main reference for soloing should be the written chords (four notes-chords and their relation with the bass).” Furthermore, he employs non-retrogradable rhythms in connection with symmetric melodic structures.
How do my analyses relate to the mentioned operations with M2 and M6? First, in the composed parts it is striking that, in contrast to the apparent presence of M2 and M6 in the majority of the chords, the bass melody rather uses M4 and M7. Second, by the abundance of notes added in the melody lines of A and B, these should rather be analyzed as (fragments of) chromatic scales. Third, concerning the solos, Orti plays embellishments of various transpositions of M2, but his embellishments of M6 are sporadic. Since during his solo the chords are played at half tempo, he succeeds to apply a chord-scale approach, matching the complex harmonic structure. His embellishments navigate between the written chords and the transpositions of the relevant modes. Van der Werf’s solo takes M2 as its point of departure for excursions to implied and neighboring harmonies by adding foreign notes to the mode. Thus, he displays an inside-outside-inside approach to the mode. Within the context of this study, this can be considered as another interesting tool to transcend the conventional chord-scale approach.
In addition to what has been said about the operations by Veras and Orti, Van der Werf adds a next step into the creative application of Messiaen’s modes. Veras quite simply demonstrated the content and structure of M3, M4, and M6, with sparse additions of notes outside of the original modes. Orti’s solo displayed the form of a chord-scale approach by obvious references to Van der Werf’s composed structures. But he also felt free to creatively embed notes that were outside the chords or outside the modes. The same freedom Van der Werf took in the composed parts of “Calcutta,” that is, to embed “foreign” notes alongside the original notes of the modes, is also present in his improvisation. In my opinion, his application of M2 convincingly illustrates how the combination of a strictly arranged mode and a freely creative approach facilitates a composing improviser to enrich the jazz idiom in a convincing way.
It should however be noted that adding too many notes to the basic transposition of a mode could cause problems. The more notes that are added to the original mode – adding two notes to M7, three to M3, or four notes to M2 or M6, changes these modes into twelve-tone rows – the more its symmetry and thereby its characteristic sound tends to be obscured. Although I am not arguing in favor of a strict approach to any of Messiaen’s modes and although I do not have objections to improvisational operations with twelve-tone scales (see chapter 4), I advise students who employ these modes in their compositions or improvisations to avoid (or to only sparsely apply) the addition of extra notes.
ex 5.3.3.3
“Let’s Give This Tree A Little Friend” (Jasper Blom) – “send off” to the tenor saxophone solo
The following example shows a transcription of Blom’s first unaccompanied solo fragment. This passage as a whole can be considered an embellishment of CM3, illustrating its various characteristic tonal colors. The brackets above the staff indicate which of the three “basic tonalities” actually dominates the line: C, E, or Ab. The parts that are encircled mark the chords that are evoked in Blom's lines.
Bars 1–8 contain repetitions and variations of a limited fragment of CM3. The whole and half notes at the end of the fragment express the tonal anchors G and F#. The tonal color of Gmaj7#5 is confirmed in bar 8. The line in bars 9–10 is disjointed because two foreign notes, f and d♭ are added. Both notes serve as chromatic passing notes. Because of the forceful ending on the a♭, this line is marked AbM3.
Just as in bars 1–8, Blom’s line in bars 11–18 never leaves the M3 mode. Due to the strong presence of once again the a♭, this time as a fortissimo-played initial note, bars 11–16a are marked as AbM3. In bars 16b–19, as a result of playing “false fingerings”, the "foreign" notes a and f are added to the line that is originally based on EM3.
The encircled parts indicate a number of chords that can be identified in Blom’s embellishments of M3. After the tonal color of Gmaj7#5 in bar 8, bars 11–19 show a variety of chords constructed on the three basic roots: Abmaj7; Cmmaj7(add#11); Em, Em7, Eminmaj7, and Emaj7add4. Beside these, the G augmented tonal color sounds again.
ex 5.3.4.1
“Prayer” (Steve Lacy) – introduction and theme
The D♭M3 mode also determines the sparse notes in the following first fragment of Lacy’s soprano saxophone solo. Here, by omitting the notes e, g, and c, he uses only six of the nine possible notes: d♭–e♭–f– a♭–a–b, evoking the augmented tonal color of D♭7#5.
5.3.3 Jasper Blom “Let’s Give This Tree A Little Friend”
In his composition “Let’s Give This Tree A Little Friend” (2014) for saxophone quartet and big band, saxophonist and composer Jasper Blom applies combinations of different transpositions of M3 and M6 in layers of contrapuntal lines. The following example displays the first sixteen bars of the melody that is formed by stacking five layers upon each other. Every time this section is repeated, another group of instruments is added.
Piano, bass and drums (not notated) start off with a descending line constructed with mode transposition EM6 (with the note c♯added), followed by an ascending line constructed with EbM6. At the first repetition, the baritone saxophone and the bass trombone play a contrapuntal line of EbM6 (ascending) and EM6 (descending). At the second half of this first repetition, first and second trombones enter their parts with contrapuntal lines that contain fragments of FM3 (a♭added) and AM3 (f♯ added). Next, both the saxophone quartet (not notated in this score) and the saxophone section of the big band appear. The alto and baritone saxophones play four different groups of four notes that are arranged in intervals of major thirds and perfect fifths. Each group can be related to a distinct transposition of M3: GbM3 in bars 1–2; BbM3 in bars 3–4 and 5–6; BM3 in bar 7; and AbM3 in bar 8.
The soprano and alto saxophones and the fourth and fifth trumpets expose the main melody which contains two transpositions of M3, in three short fragments and in prime forms: EM3 in bars 1–3; AM3 in bars 4–5; and again EM3 in bars 6–7. Because AM3 belongs to the same mode as FM3, the melody can be considered as a construction of two transpositions of M3 at a minor second distance. Thus, it reflects the structure of the rhythm section and the lowest horns, but with EM3 and FM3 instead of EbM3 and EM3.