Proto-scores: Explorations of Ambiguous Specificity

Einar Torfi Einarsson

The following text deals with the piece Underdetermined Figures (for any combination and kind of instruments). The piece is part of the Proto-Objects project and is here treated in its manifestation as a piece for string instruments.

Introduction

For some time, I have been exploring means to develop notations that build upon prescriptive notation of physical parameters and, importantly, notations that do not pertain to a single instrument or instrument group. I have been calling this ‘notations of general physicality’ and the aim was to fuse ambiguity and specificity; that is, there should always remain instrumental ambiguity within this notational structure, while the instructions should always be specific no matter which instrumentalist attempts to read the score.

When I was asked to be part of the Proto-Objects project, I immediately connected these earlier ideas to the concept of proto-objects. The project operates with figures (henceforth p-o-figures) that are translated into different disciplines – we could say different contexts – and I saw my involvement as somehow continuing this function of the project within my context; that is, exploring the concept of the proto-objects within the context of music. Proto-objects refer to shapes or figures that are dependent on context – figures or objects that are not yet identifiable. In my case, context is understood as a general musical context (different from, for example, a visual art context) and a specific musical context, such as string instruments. The work undertaken, which is in fact many pieces in one (multiplicity composition), explores thus the p-o-figures within a specific notational context that can mean, sound, and communicate different things when situated in different instrumental contexts. Importantly, this is not done with general musical parameters such as pitch and rhythm but with physical parameters (movements, speed, pressure, etc.). In this way I explore the behaviour of the project itself on a smaller or microscopic scale. The result is something I call a proto-score, as it is a score that awaits specific context to become an actual score (and actual music). A proto-score relies on a relationship to become actual; without a relationship (an instrumental/physical context), it is virtual – a field of all possible connections or inclusions. Naturally, therefore, the notation, the score, or the piece as such does not have a sonic identity; it does not aim for similar results (sameness, repeatability, representation, identity). In fact, it aims for dissimilar results (difference, multiplicity) in each of its performances, both in the domain of sound and action and in its presentation.

Each instance of the piece will create a different event on the basis of its context. This contextual variable or difference covers both (1) instrument groups – that is, the piece can ultimately be performed on any kind of, any number of, and any combination of instruments – and (2) performer approach, as it is possible to read through the score and each of its figures in many different ways. For this reason, the score does not provide many detailed instructions that would favour a specific instrument group; therefore, it employs abstract parametric-space notation where parametric change can refer to different physical actions/movements, depending on the instrument employed. Thus, the score is in fact a proto-score.

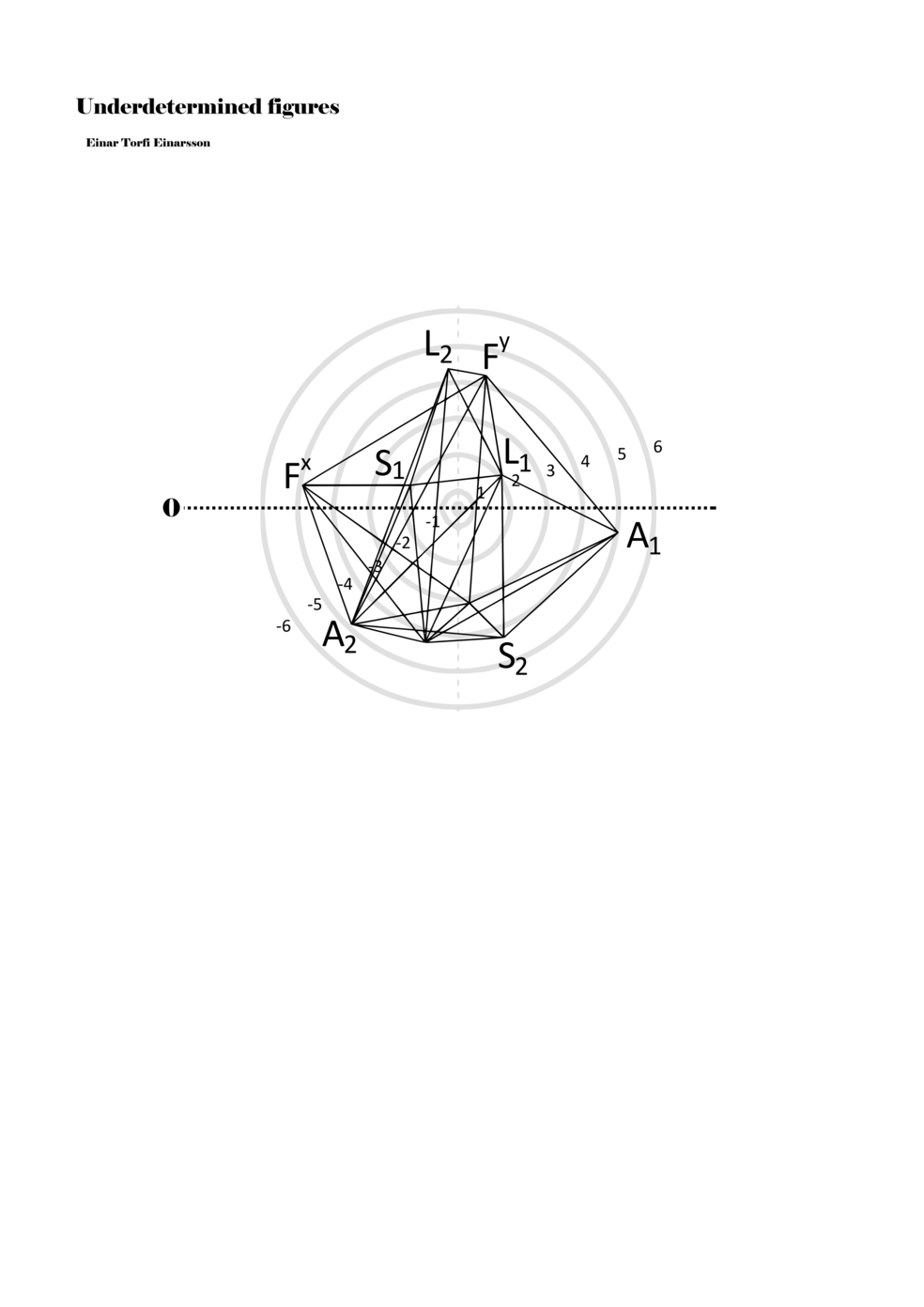
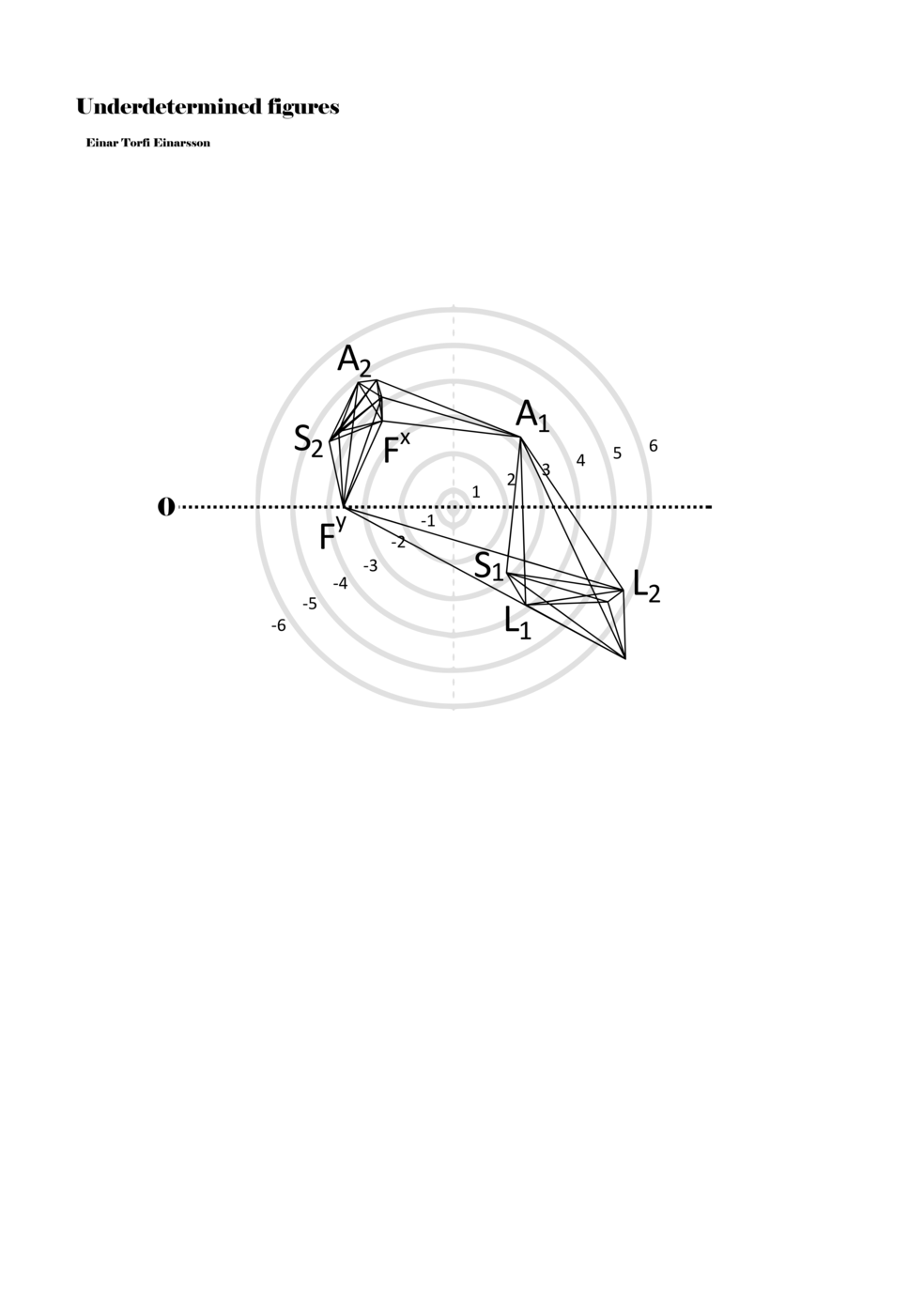
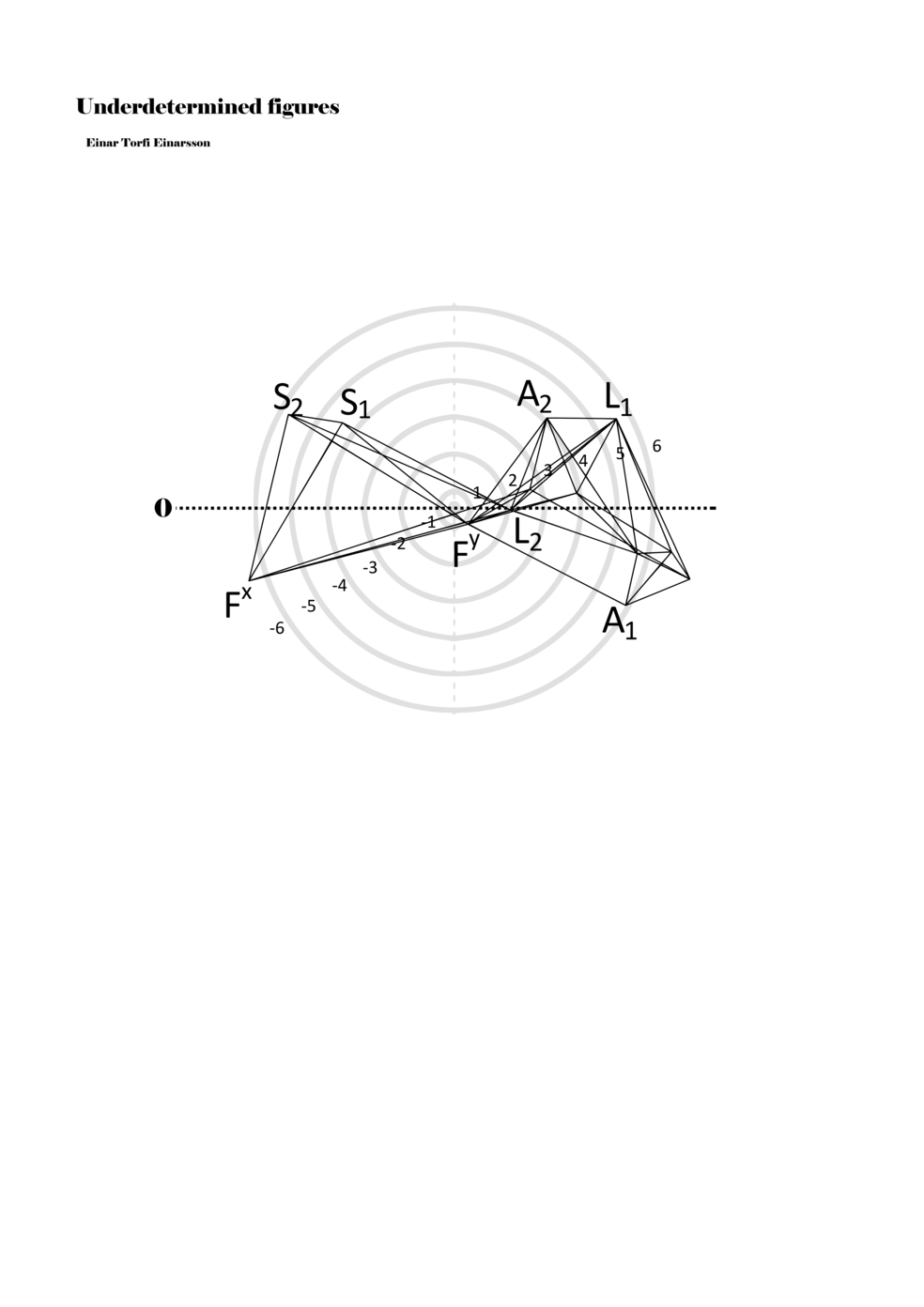
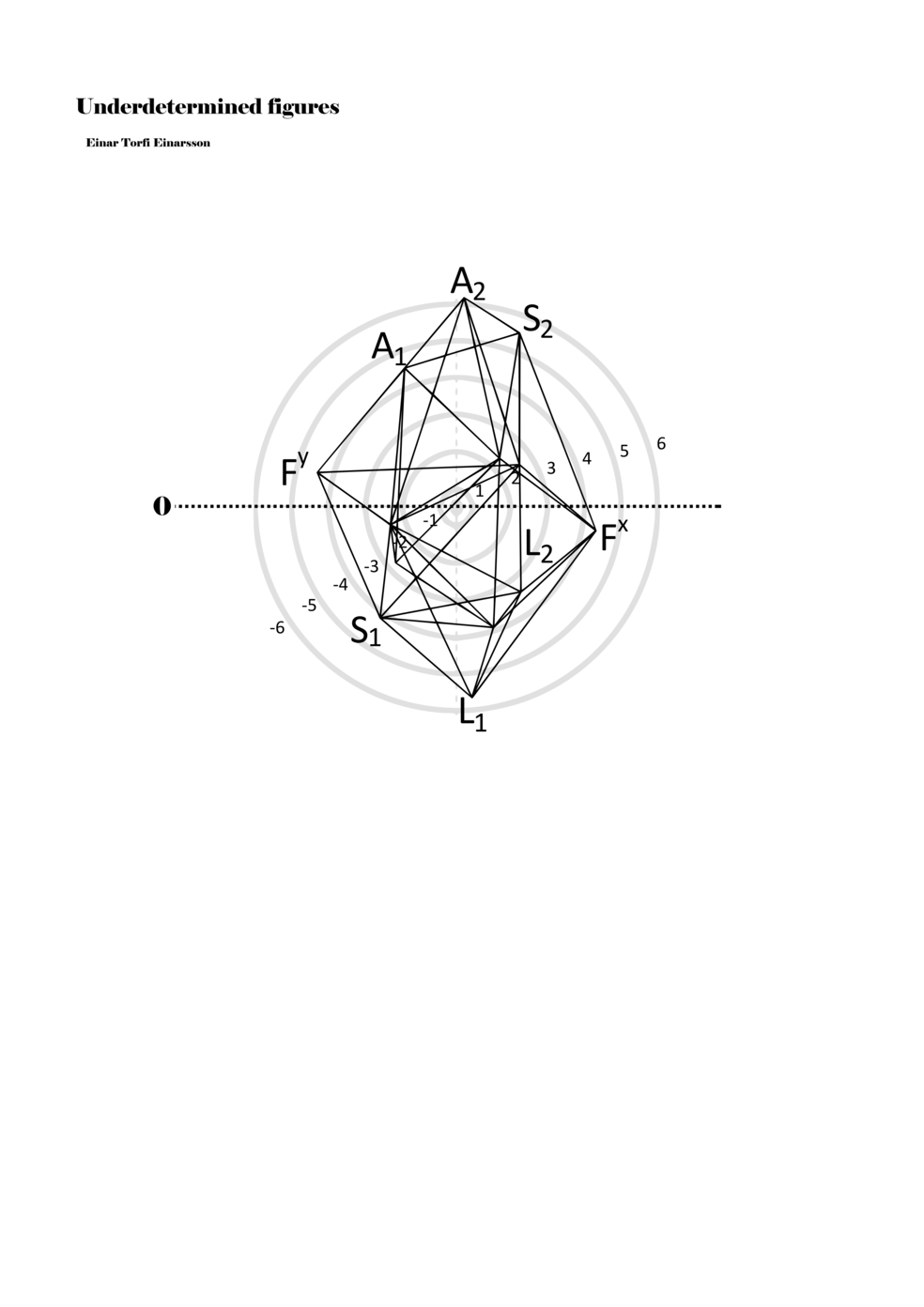
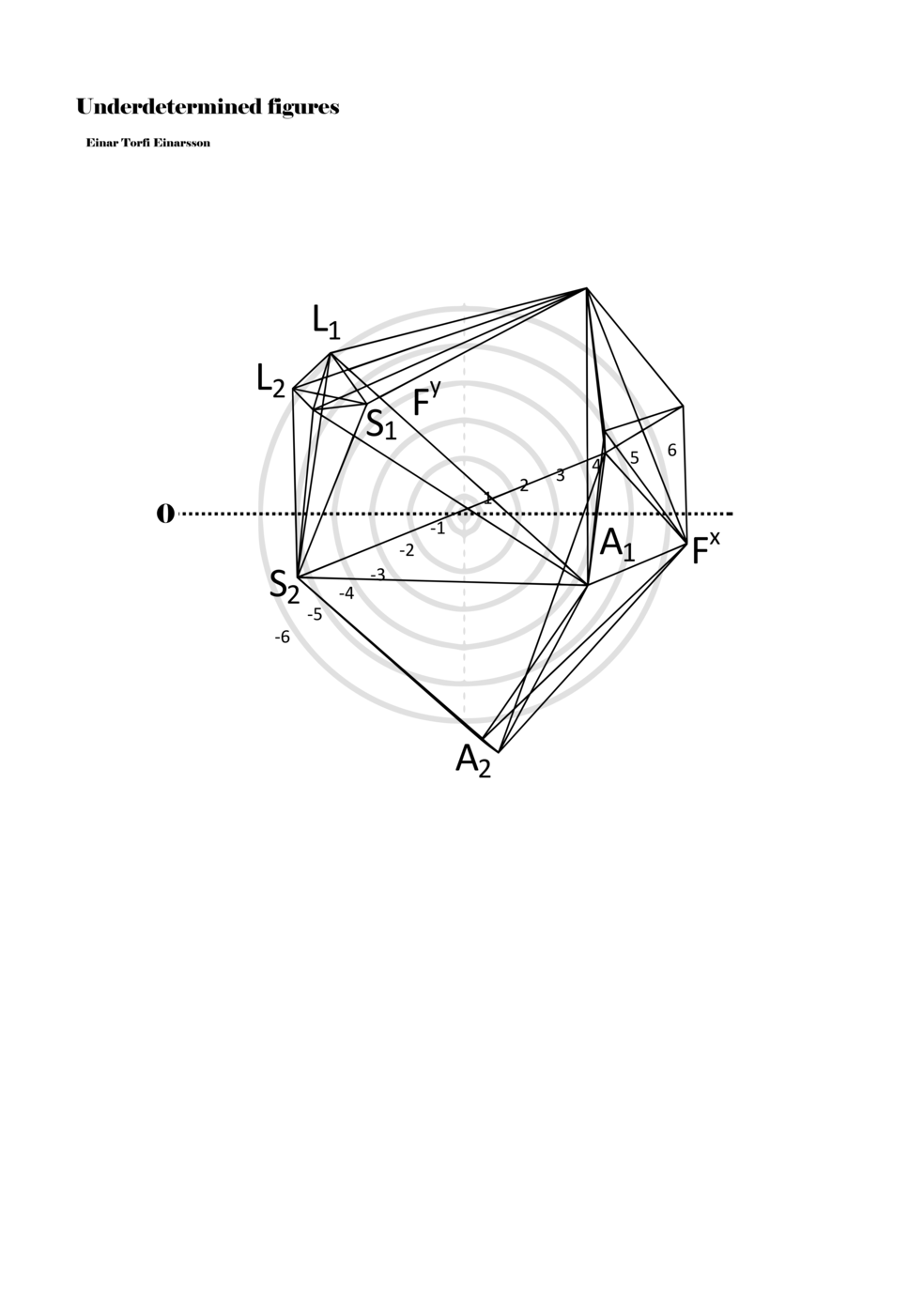
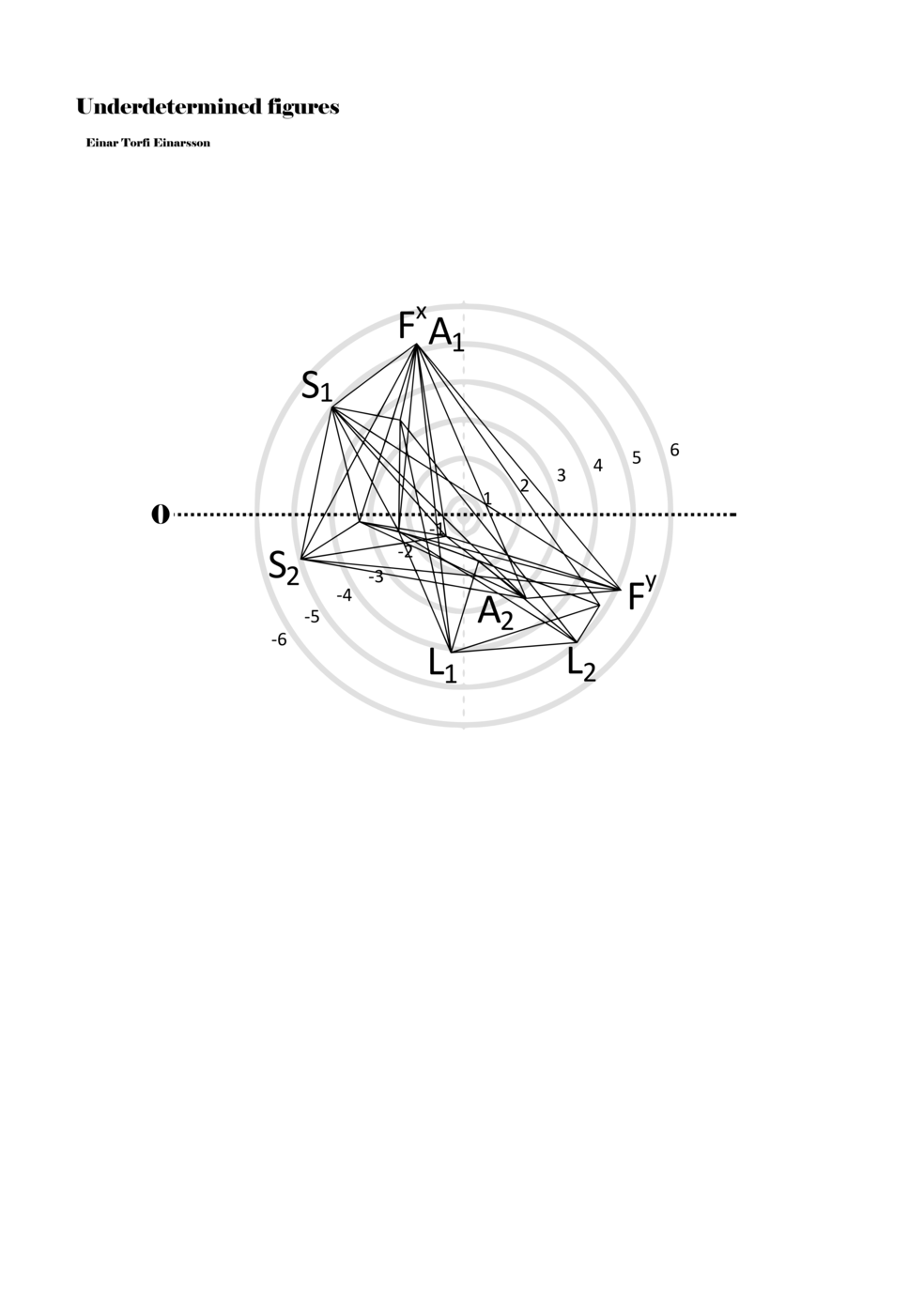
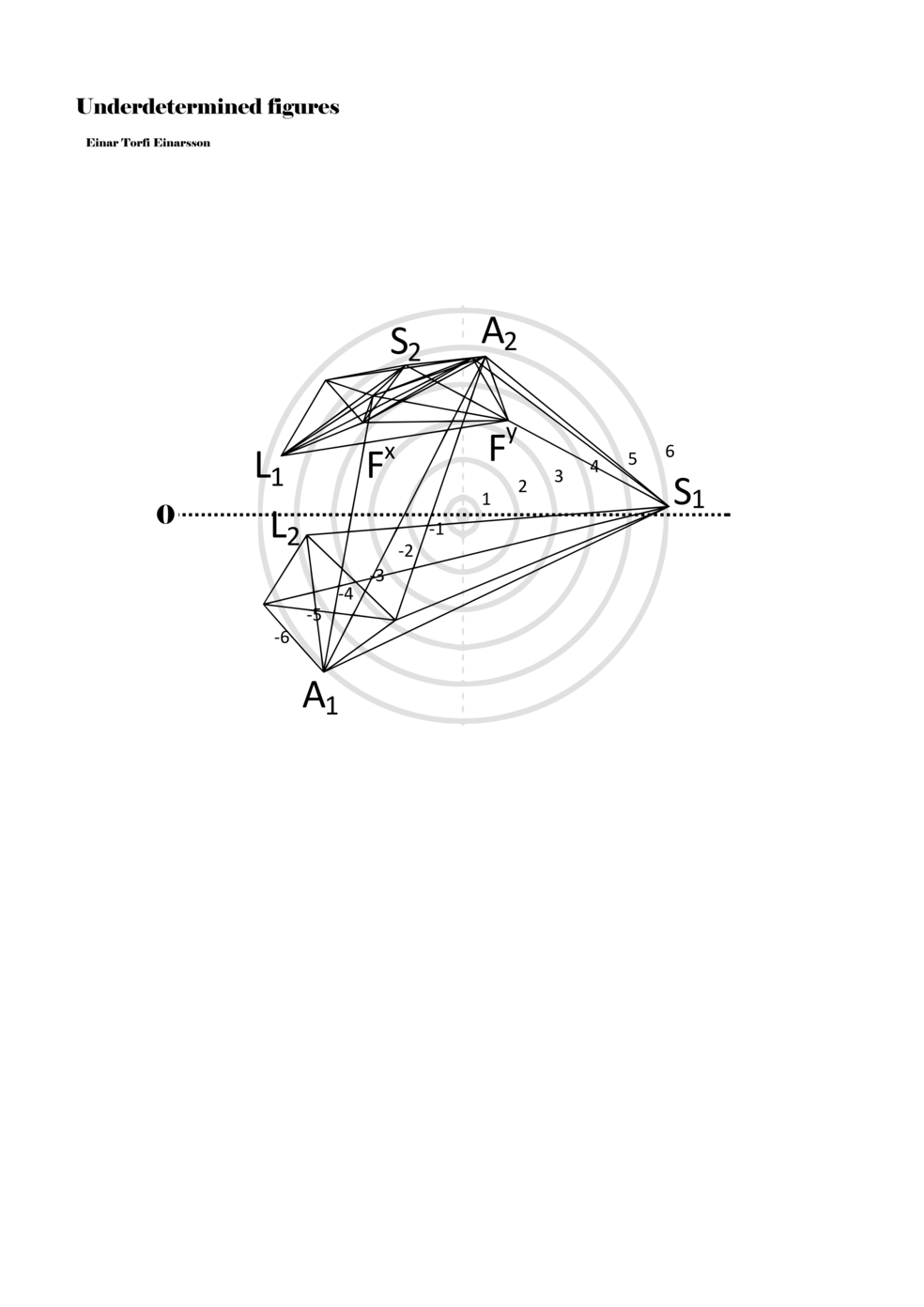
Being fascinated by the p-o-figures derived from the data of the EEG scan of the Proto-Objects project, I set out to find ways to include them in my work as notations. On the basis of the data from the EEG scan, one hundred three-dimensional figures were derived; however, for the purpose of Underdetermined Figures, one hundred two-dimensional figures were derived from the three-dimensional figures. It was also necessary to limit the number of connections between points in the p-o-figures in order to adapt it as a material for performative instructions. Thus, the figures included in my work are aspects or perspectives on the three-dimensional figures. Although the figures within the score are two dimensional, the notational context transforms them into multidimensional ‘musical objects’ that indicate abstract physical movements or parameters. As such, proto-scores can be understood to be constellations of abstract distances, localities, movements, connections, and thresholds. Proto-scores are specific (even detailed) yet underdetermined and virtual (until actualised in a particular context).

What follows is a delineation of how the score works and, in particular, how it works for string instruments; but first some general information about the piece is necessary to understand the work:

• It consists of one hundred figures, each performed for the duration of two seconds, followed by a pause.
• The duration of the piece is open-ended (not all the figures have to be performed).
• The order is not fixed (figures can occur in any order).
• The instrumentation is open-ended (from a solo to a whole orchestra).
• The presentation format is open (concert, exhibition, installation).

Many of these factors are left to the performer’s discretion. A performer can thus choose which figures to include in his or her performance and the order of those figures in performance. The figures themselves reflect these structural aspects: there are multiple ways in which they can be read, interpreted, and approached, and therefore multiple ways in which they can be repeated (within a single performance or between many performances) with different results. In the case of a non-solo performance, performers are not obliged to perform the same figures in the same order or even start together (although that is also not prohibited).

Figures become notations

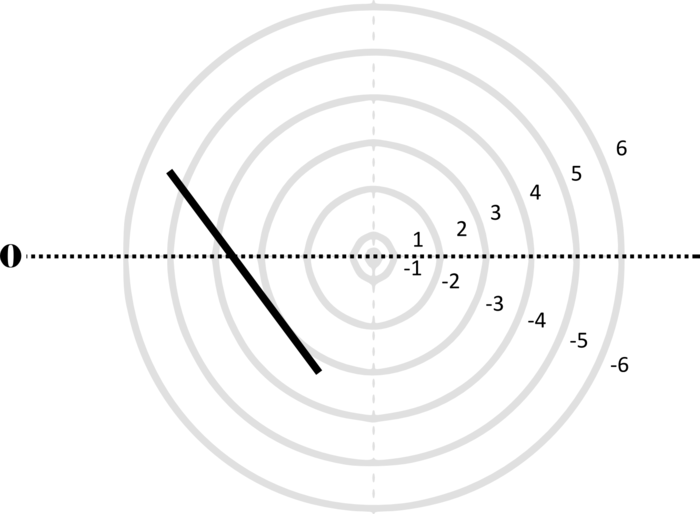
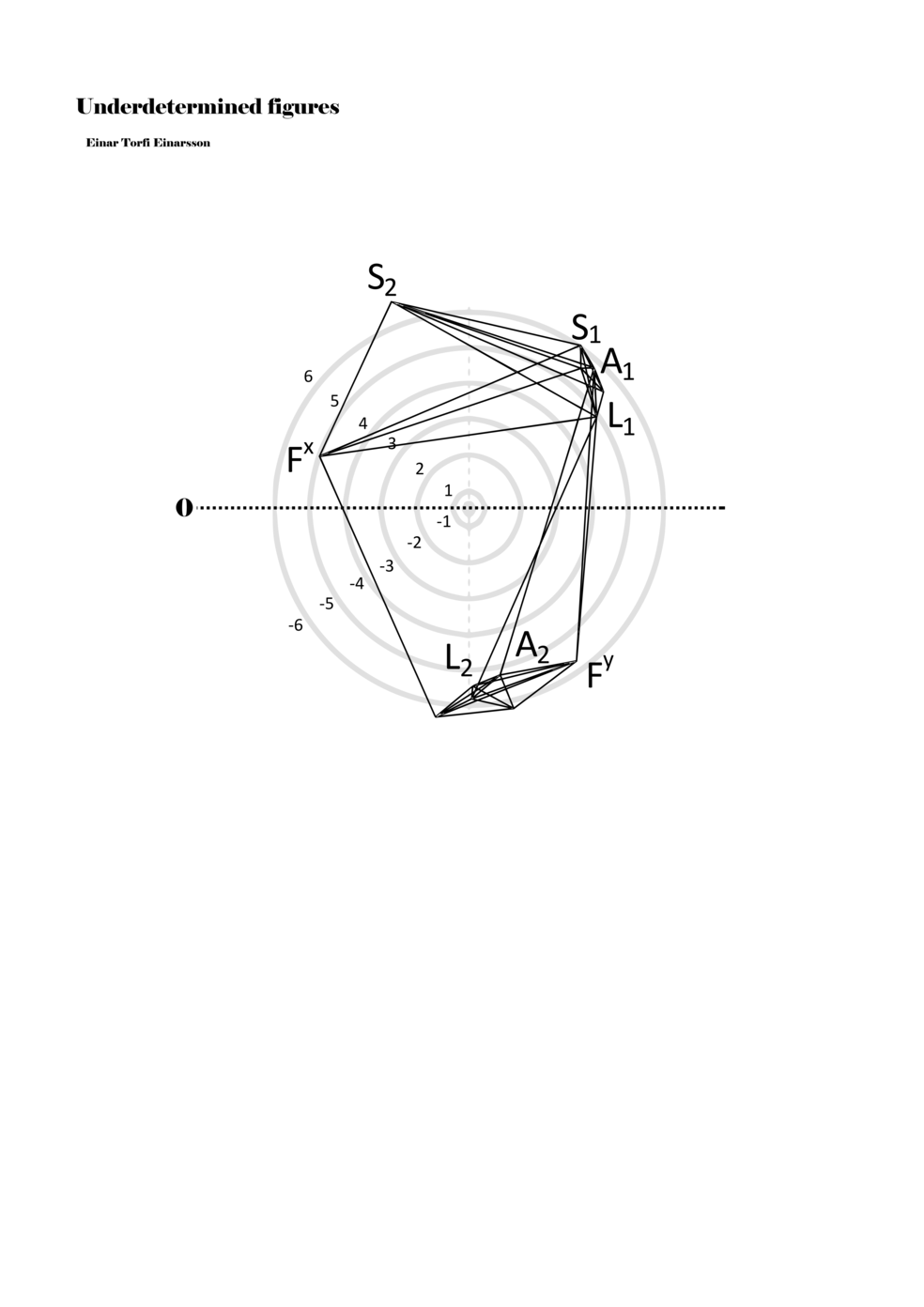
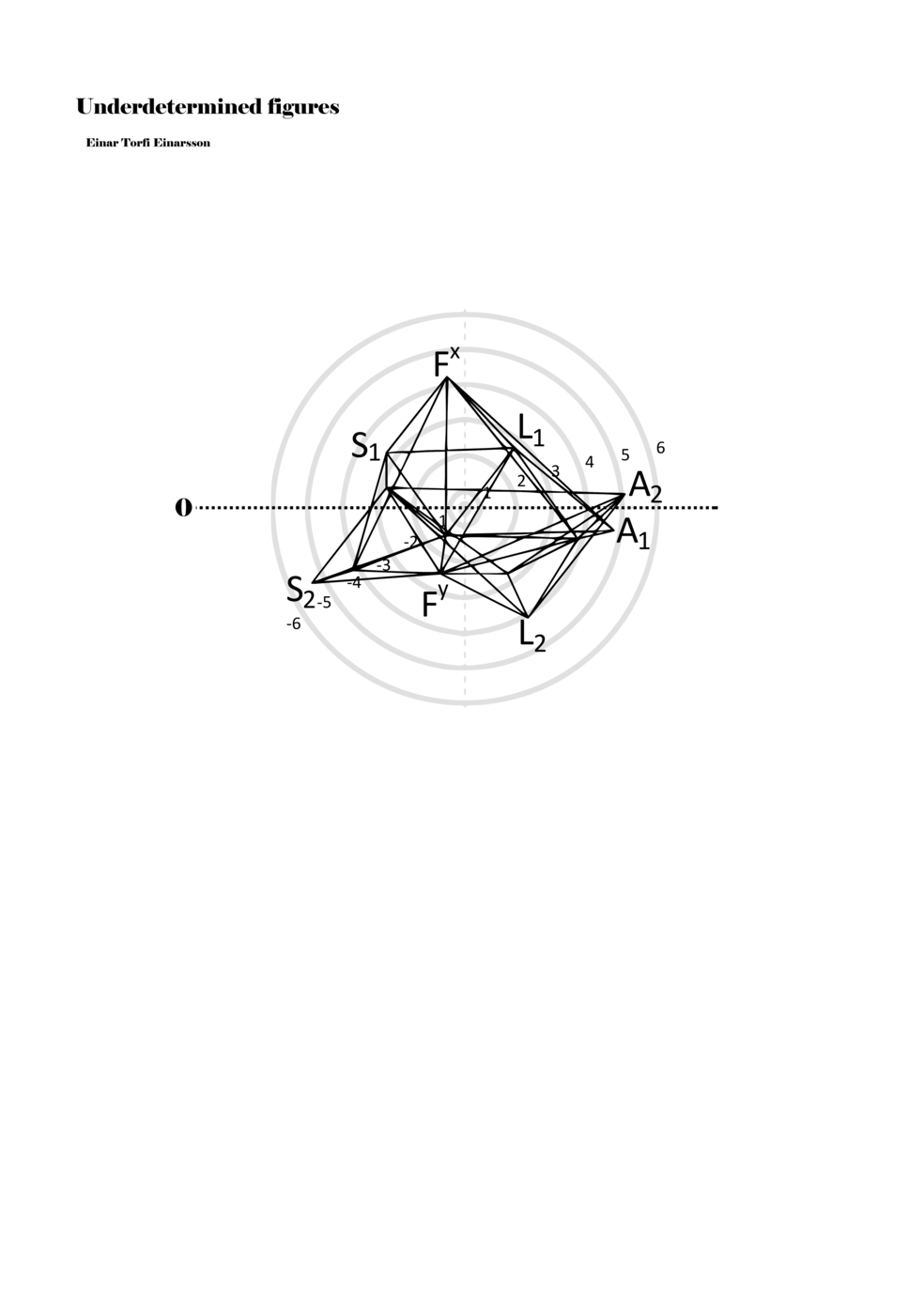
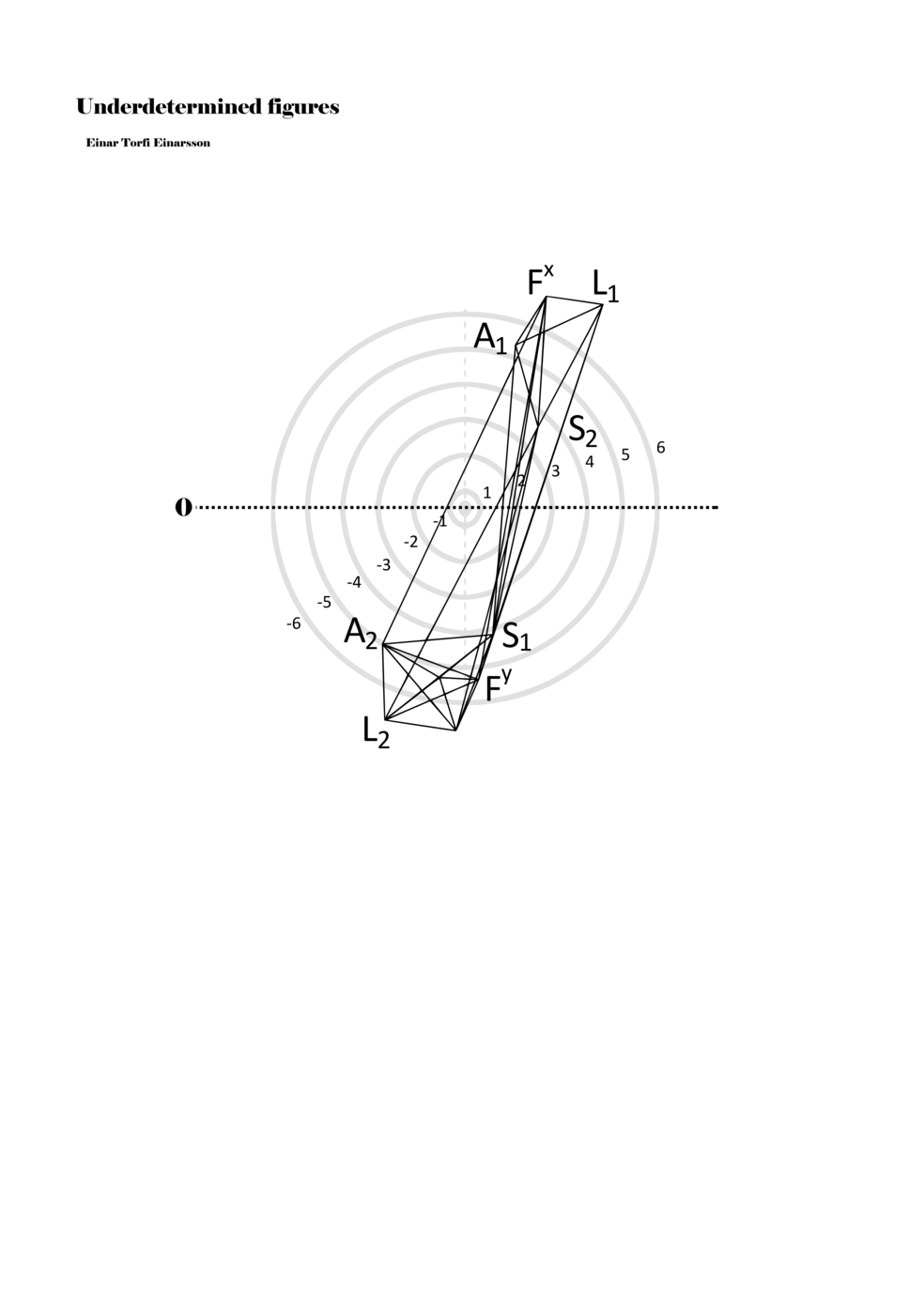
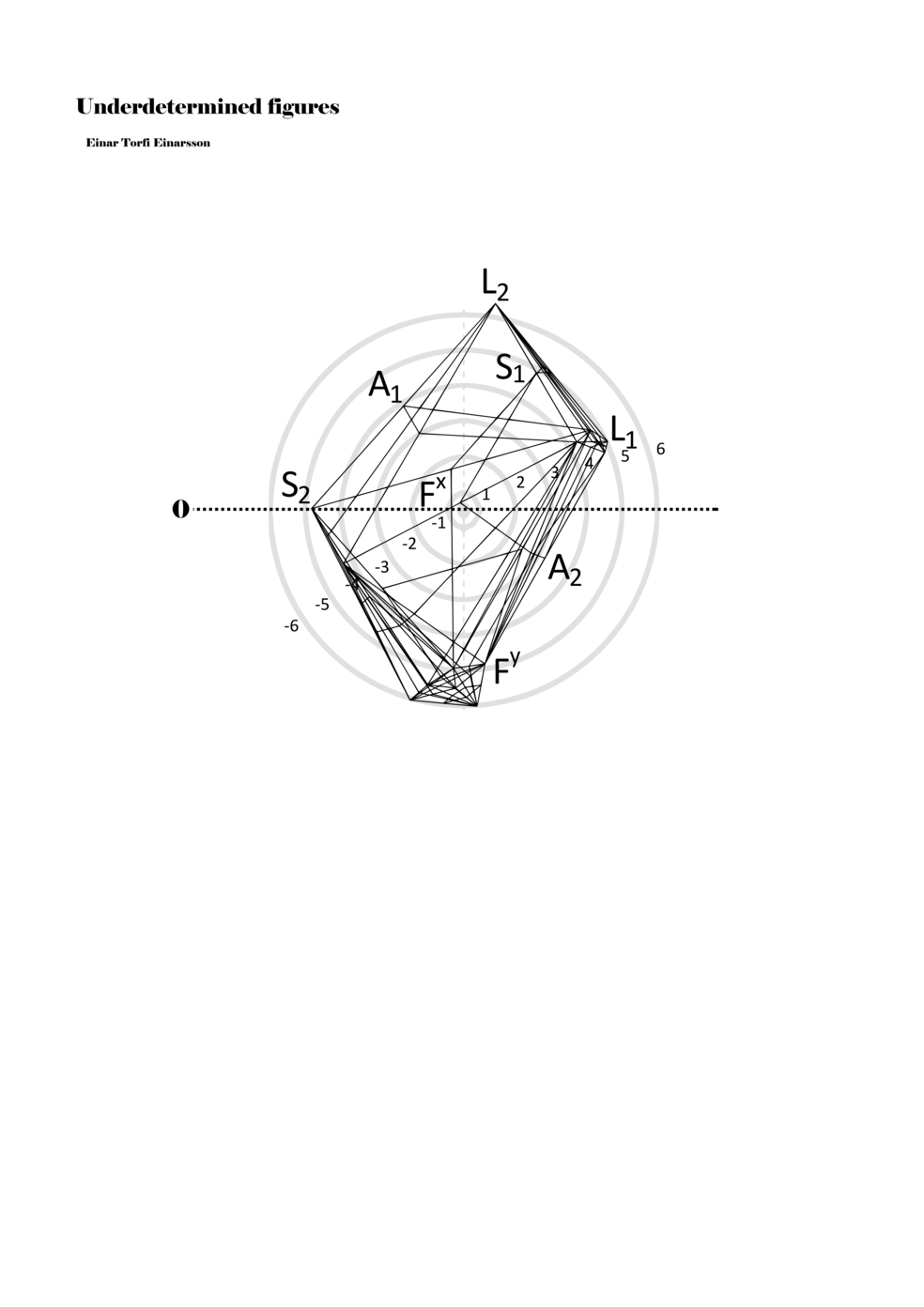
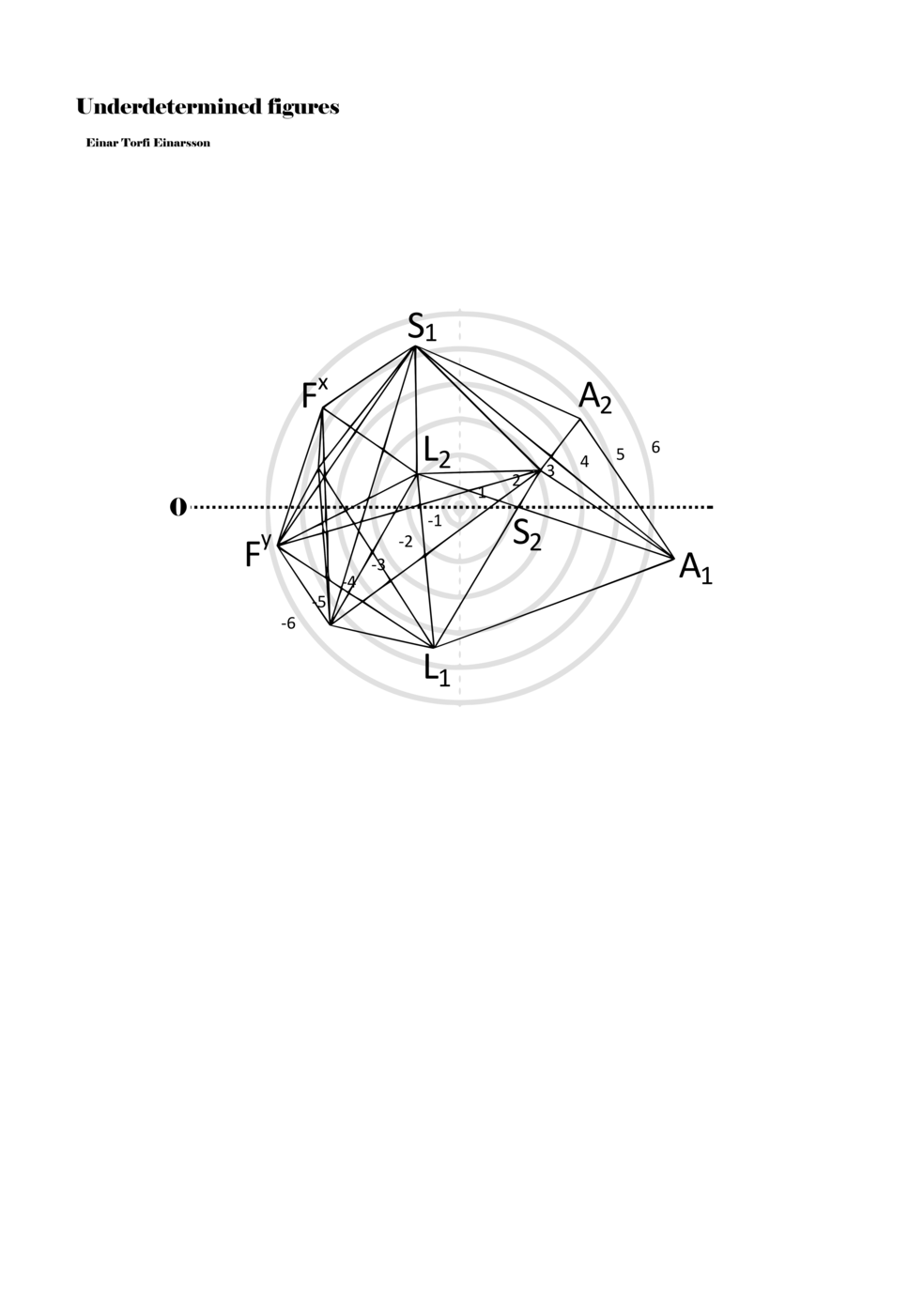
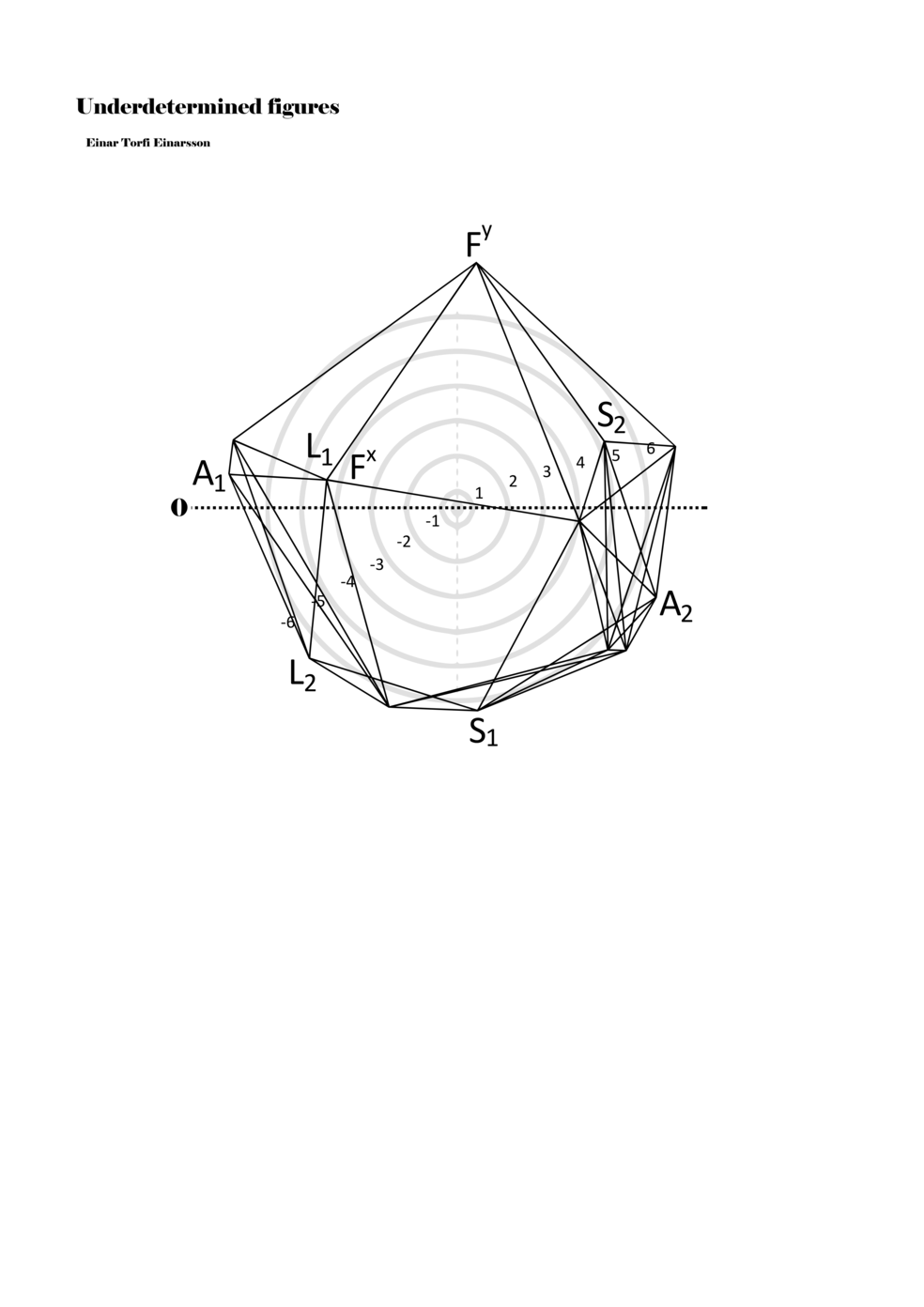
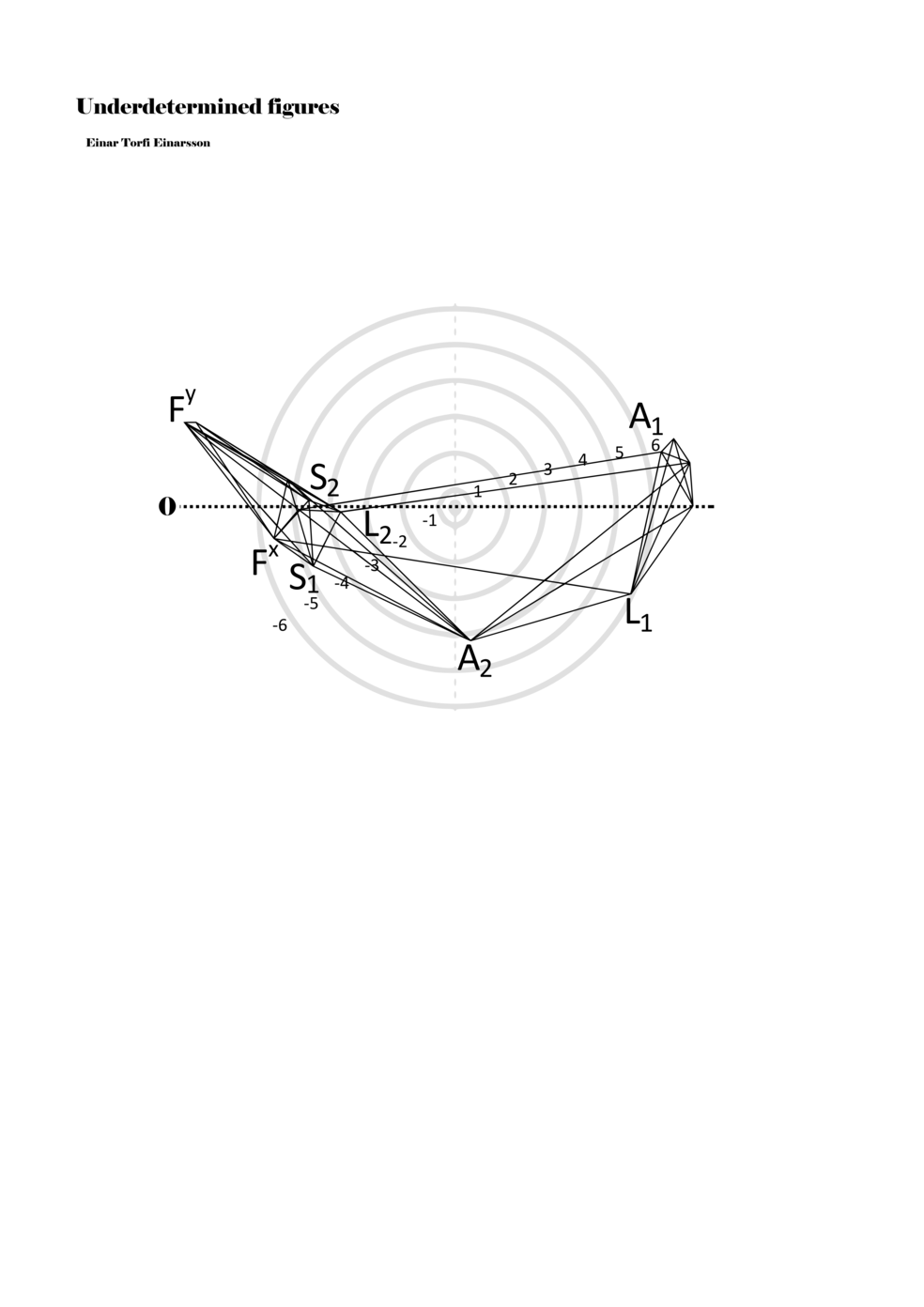
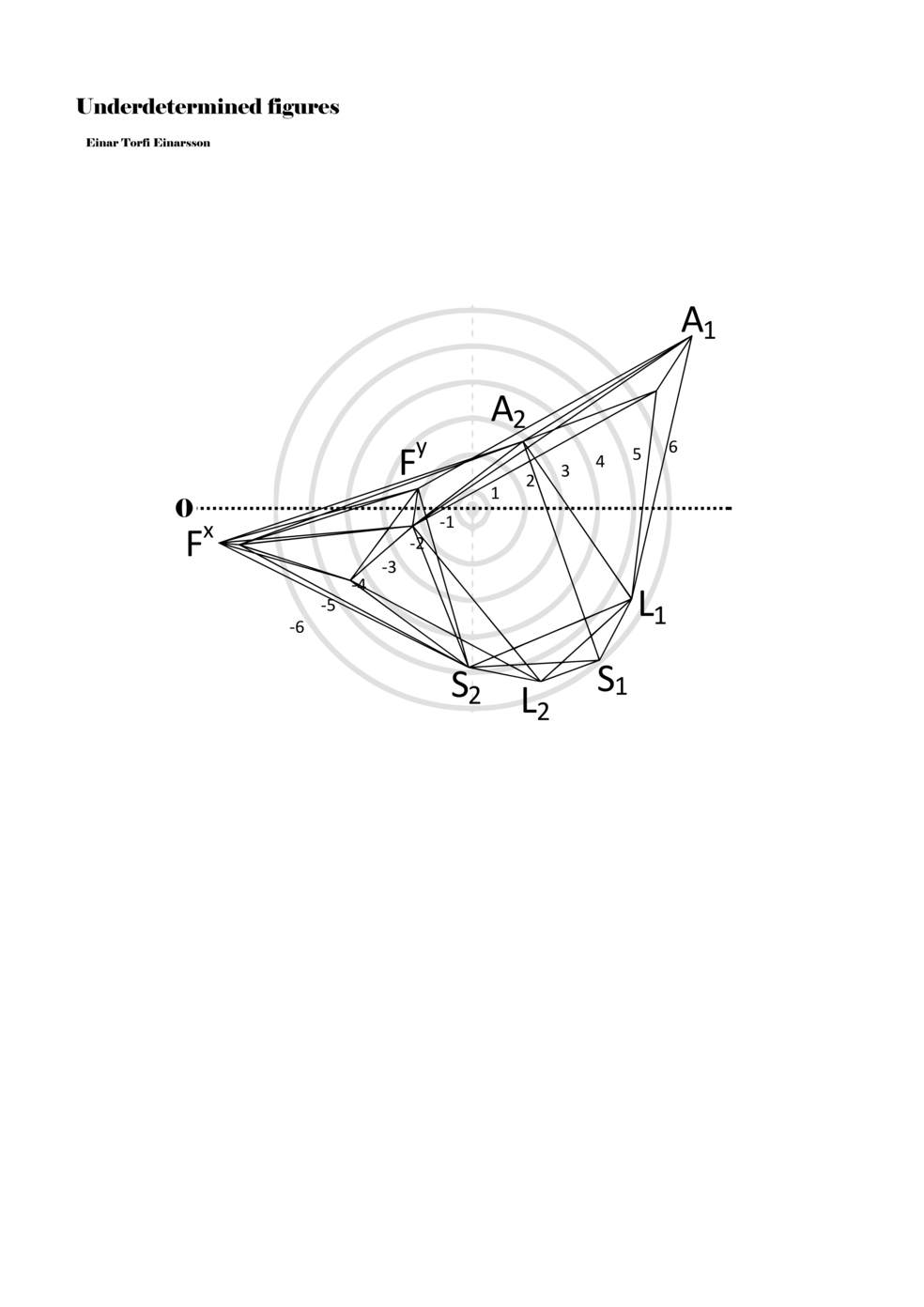
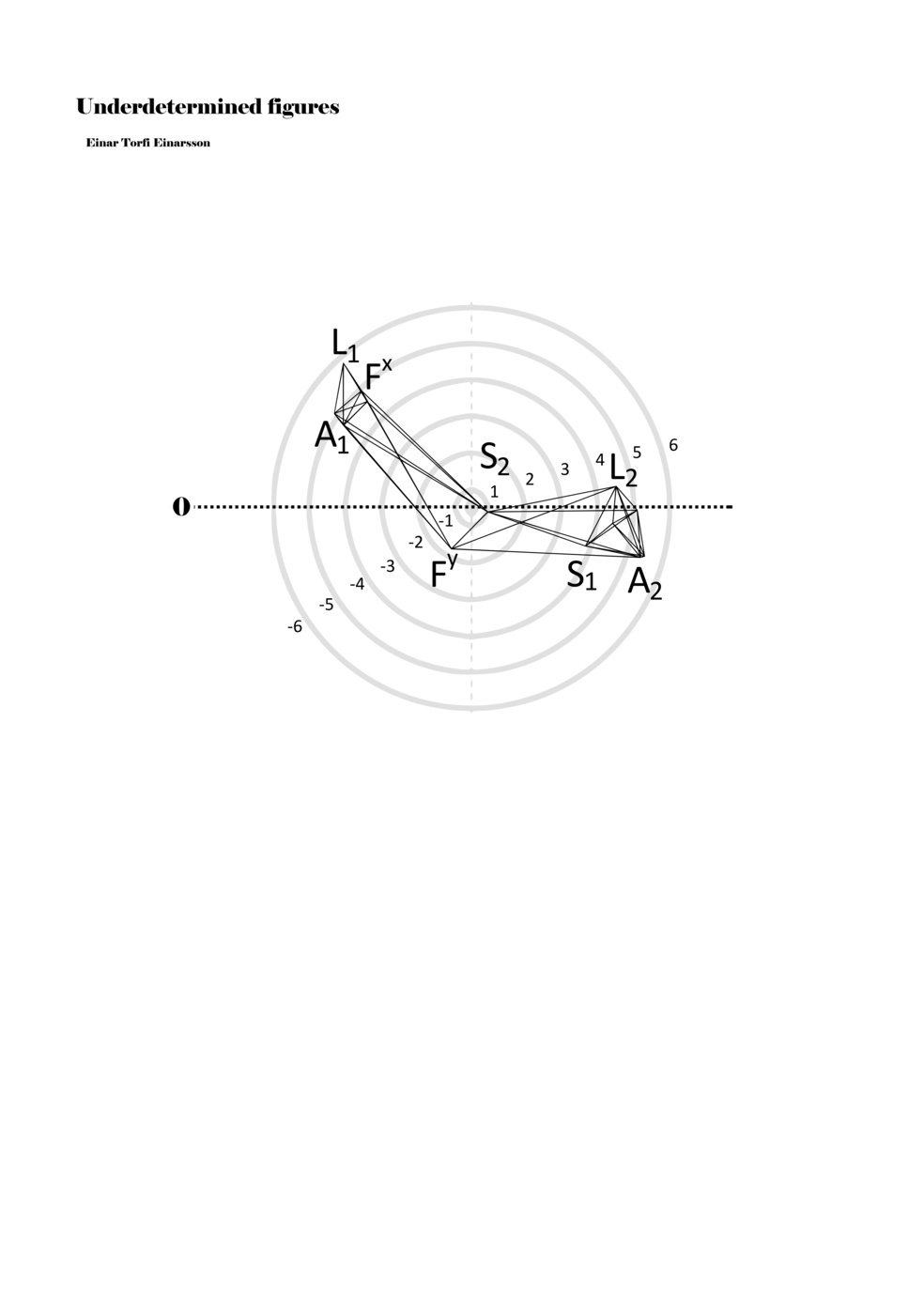
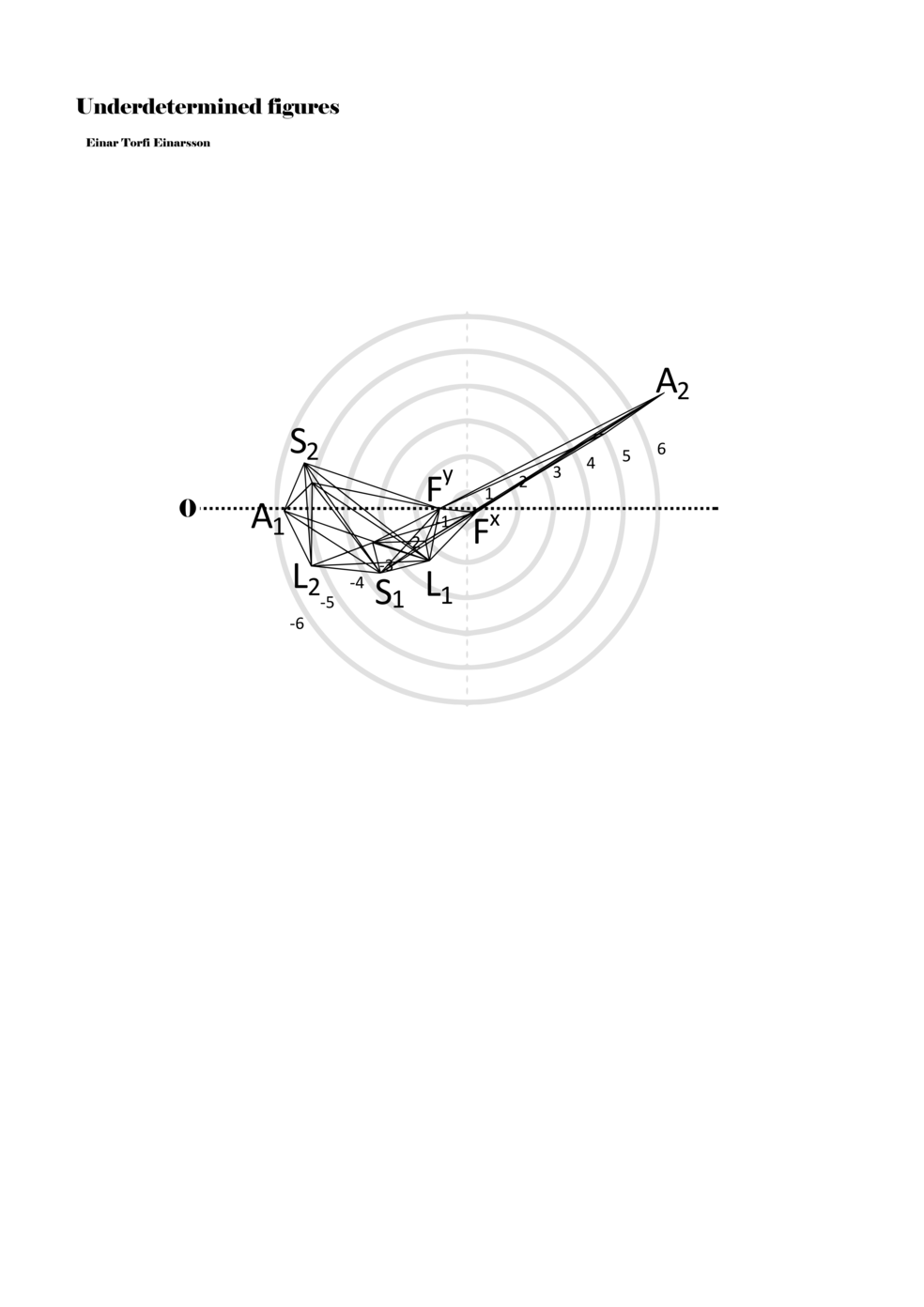
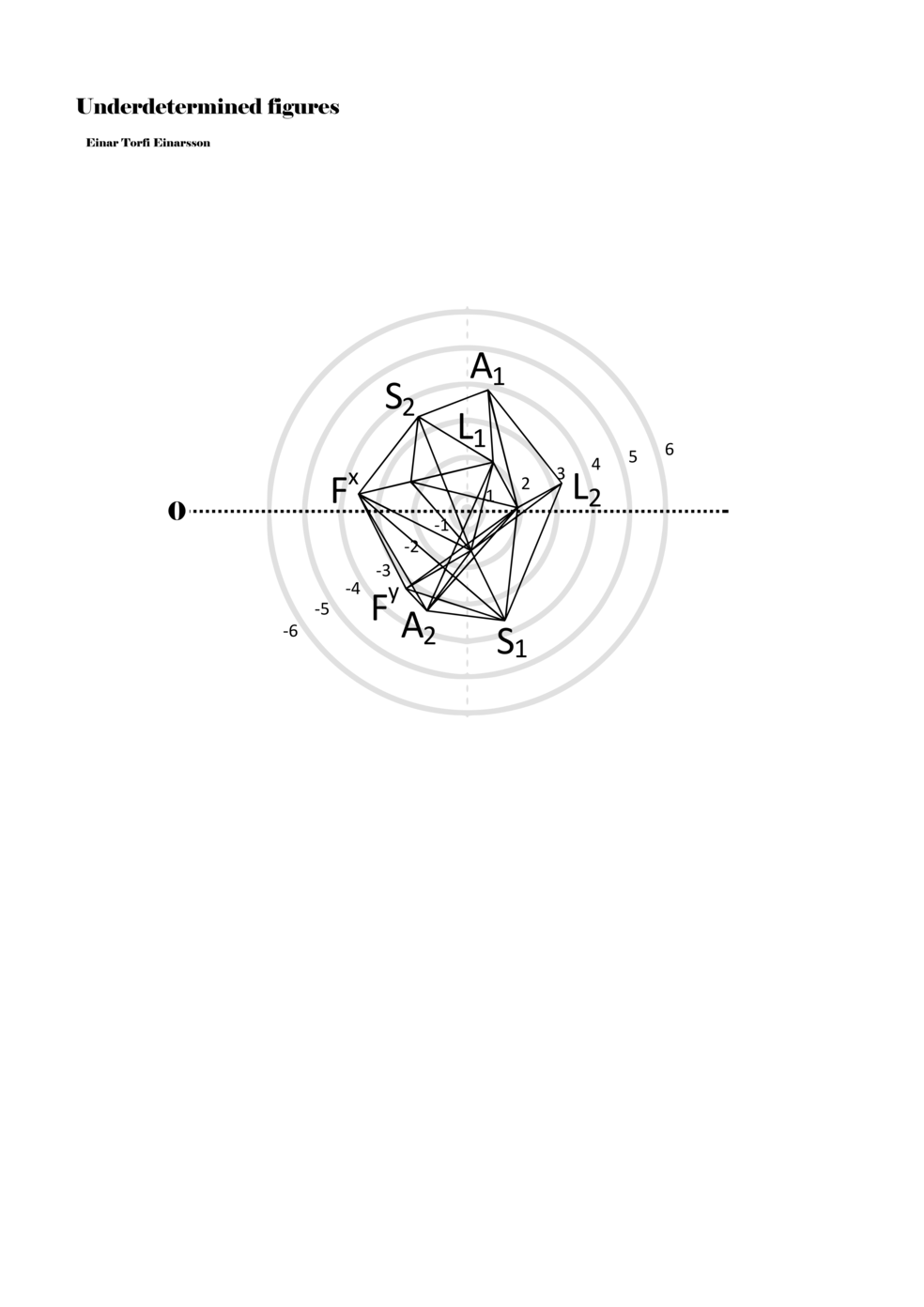
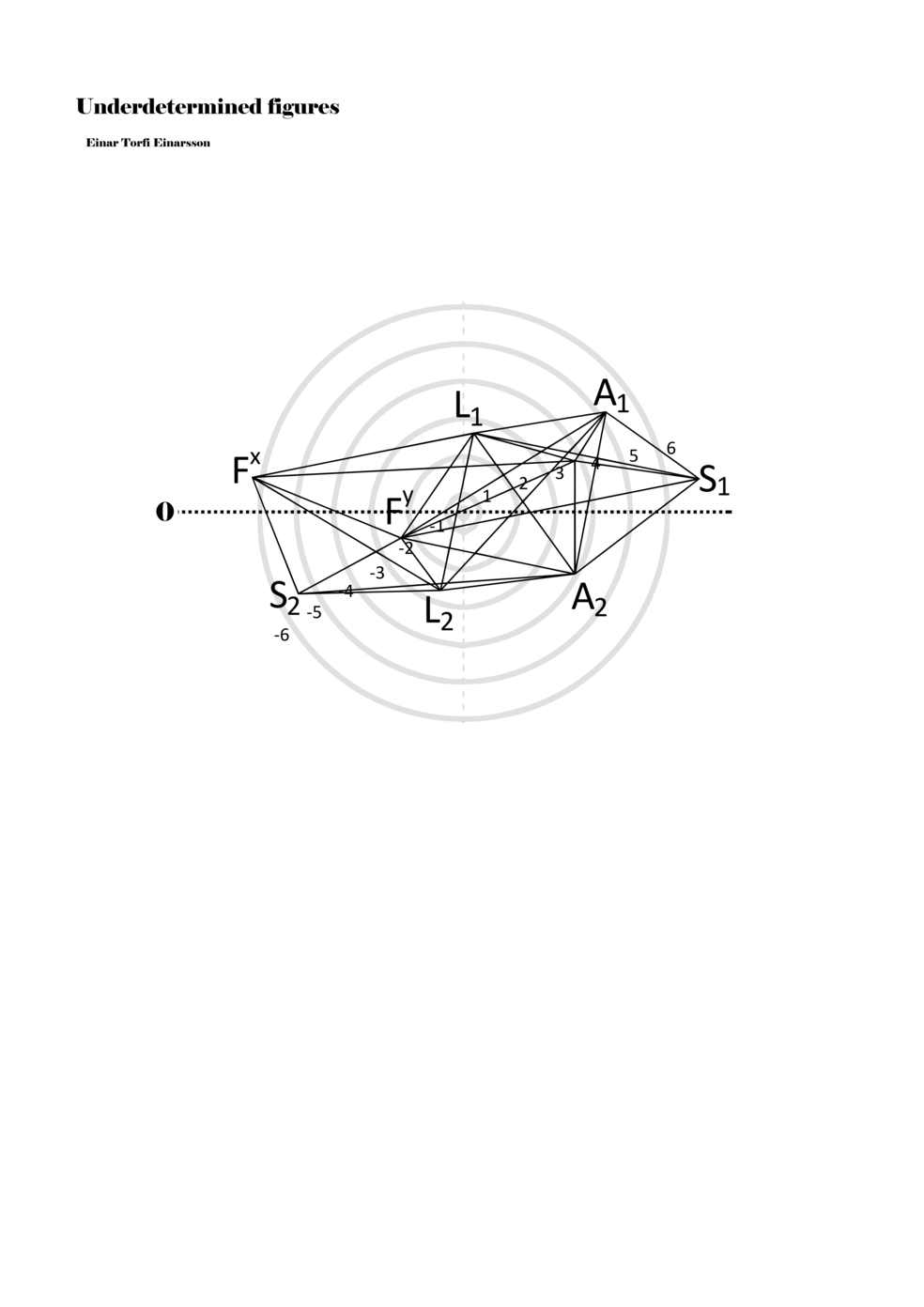
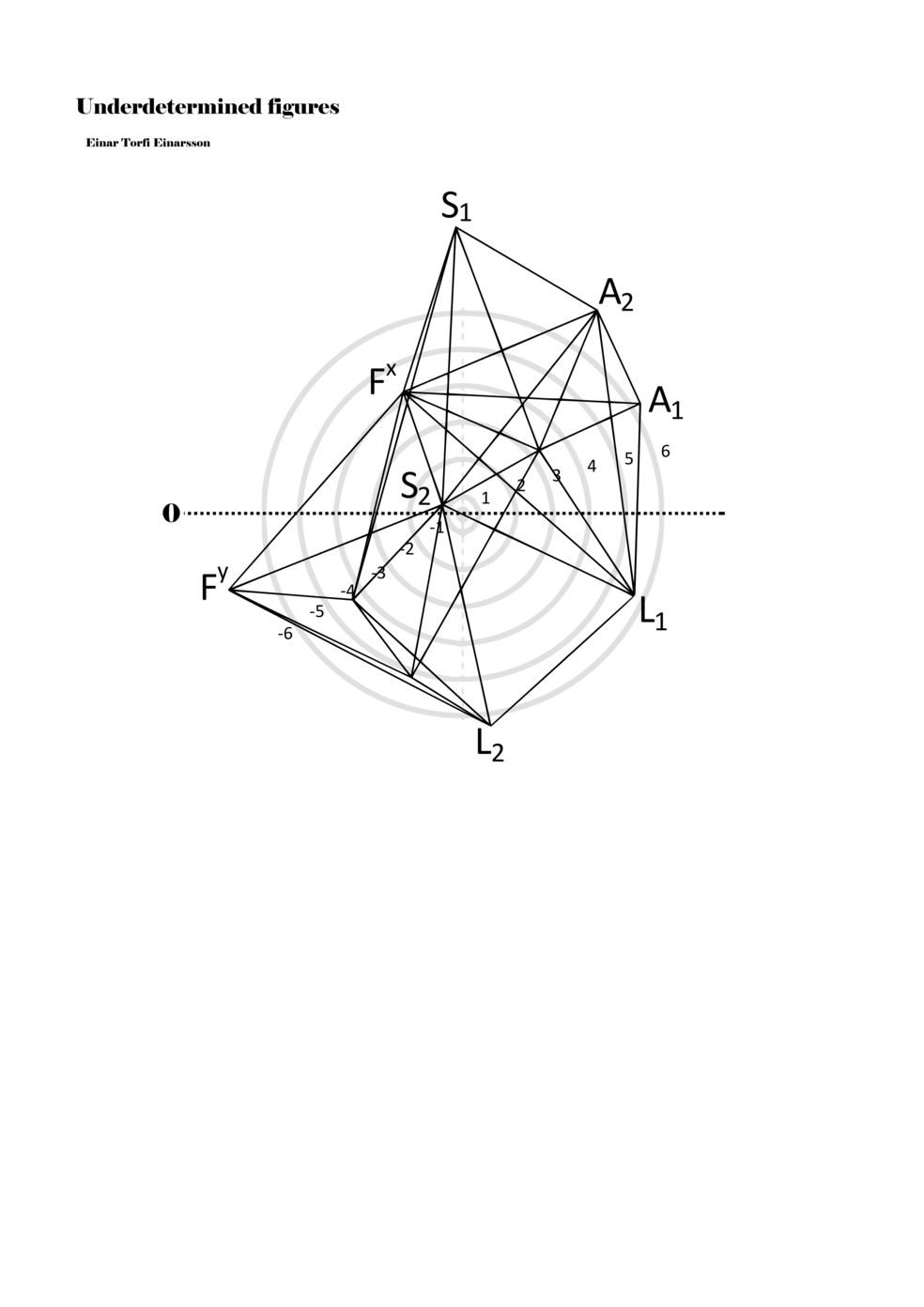
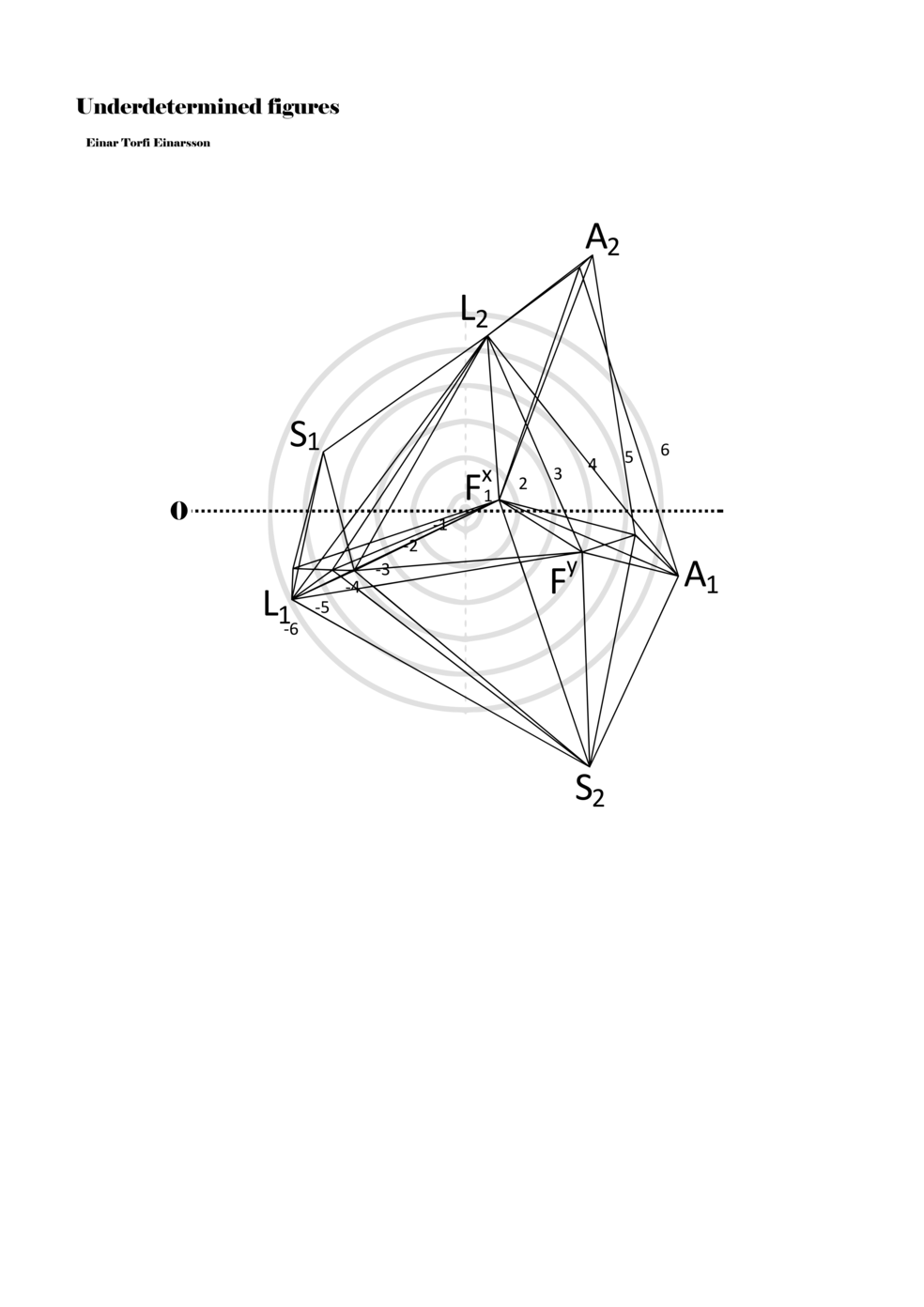
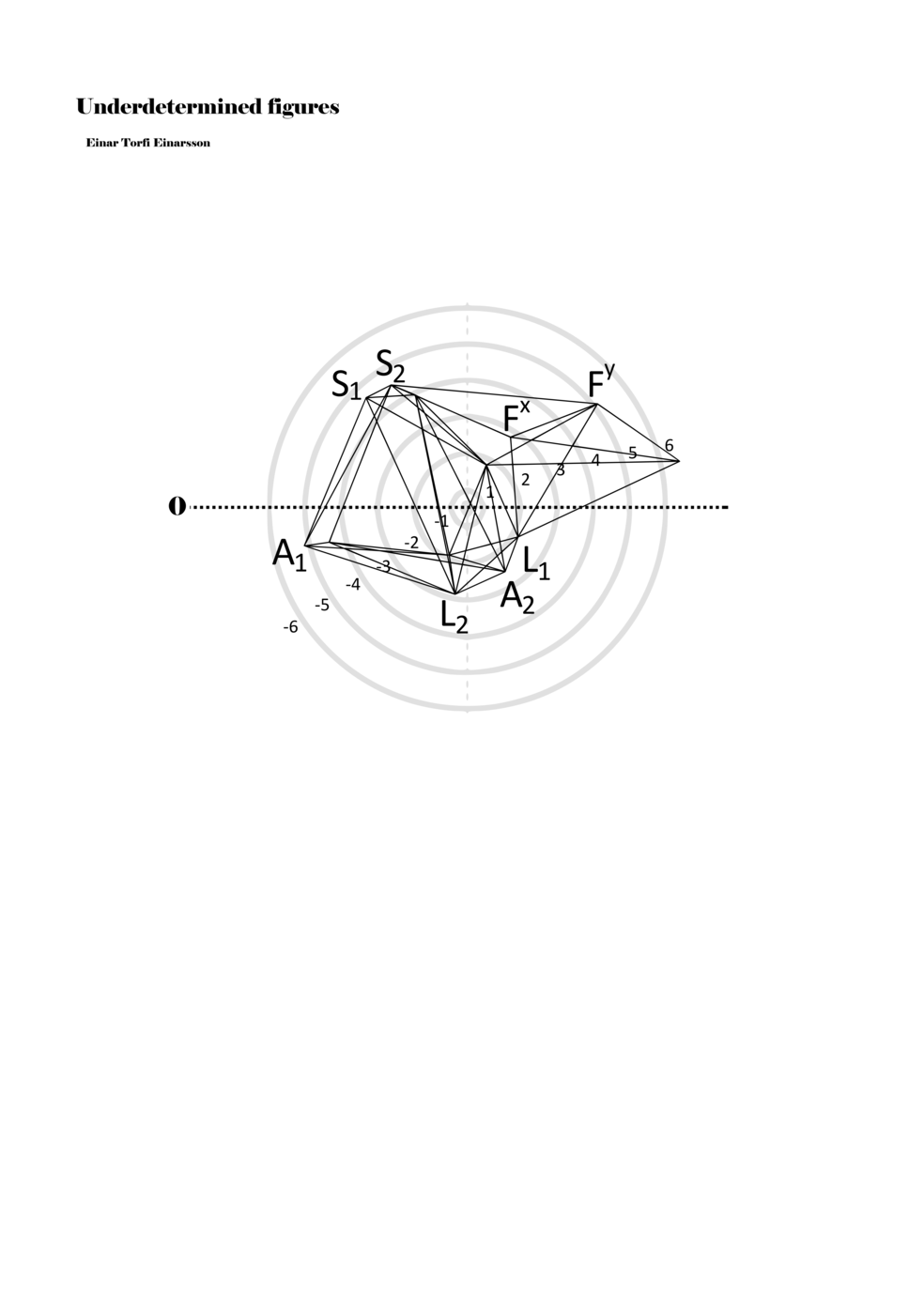
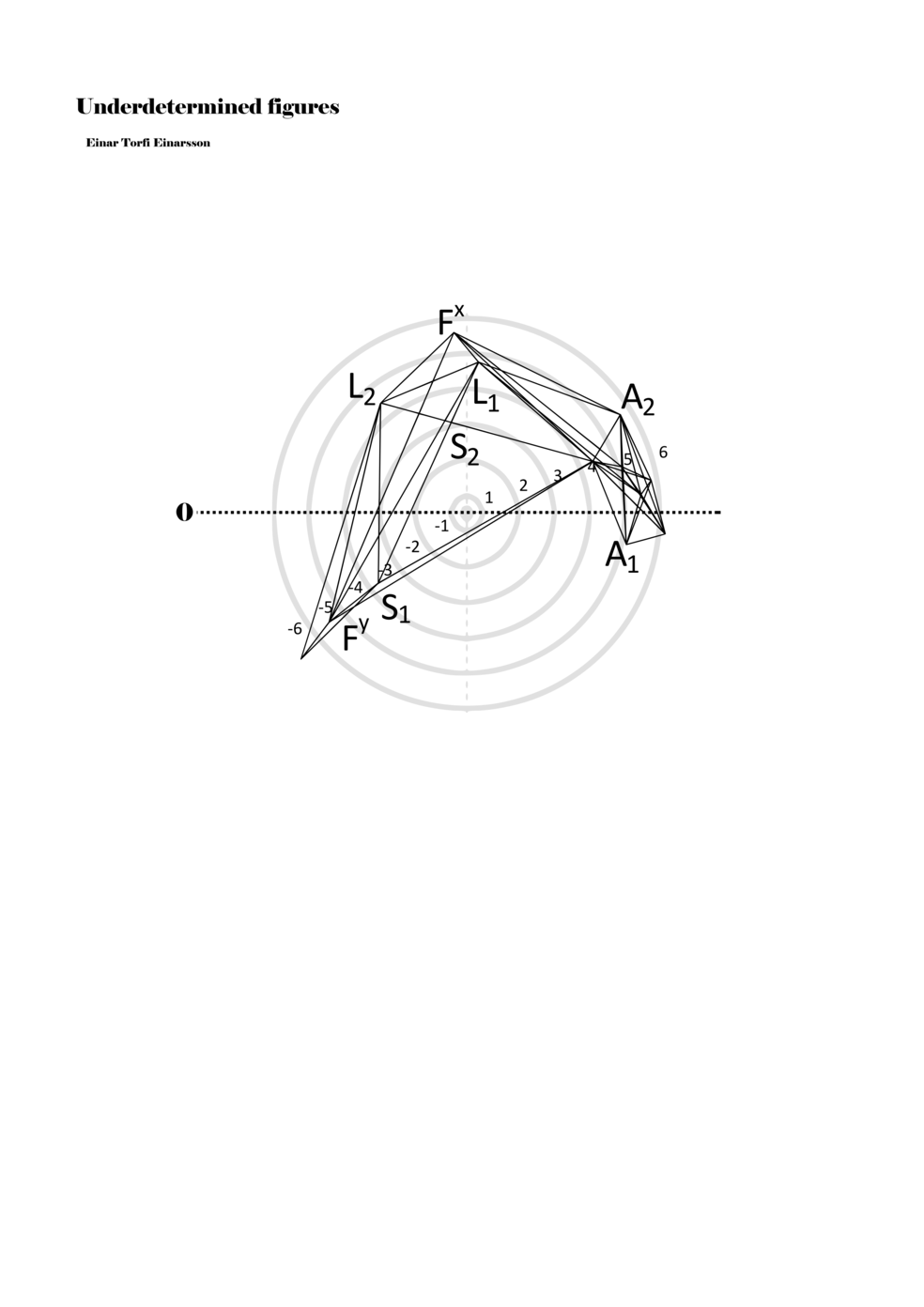
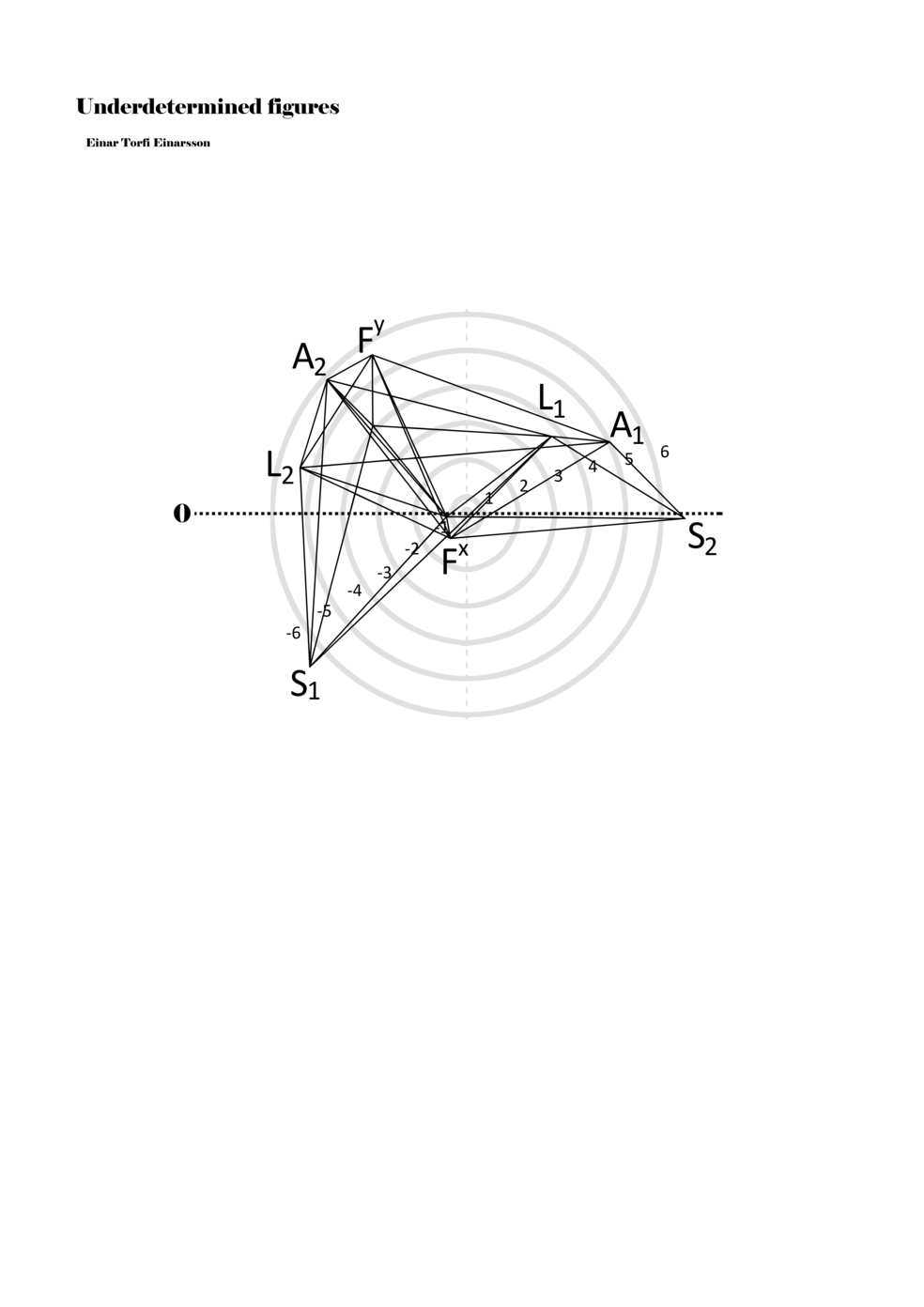
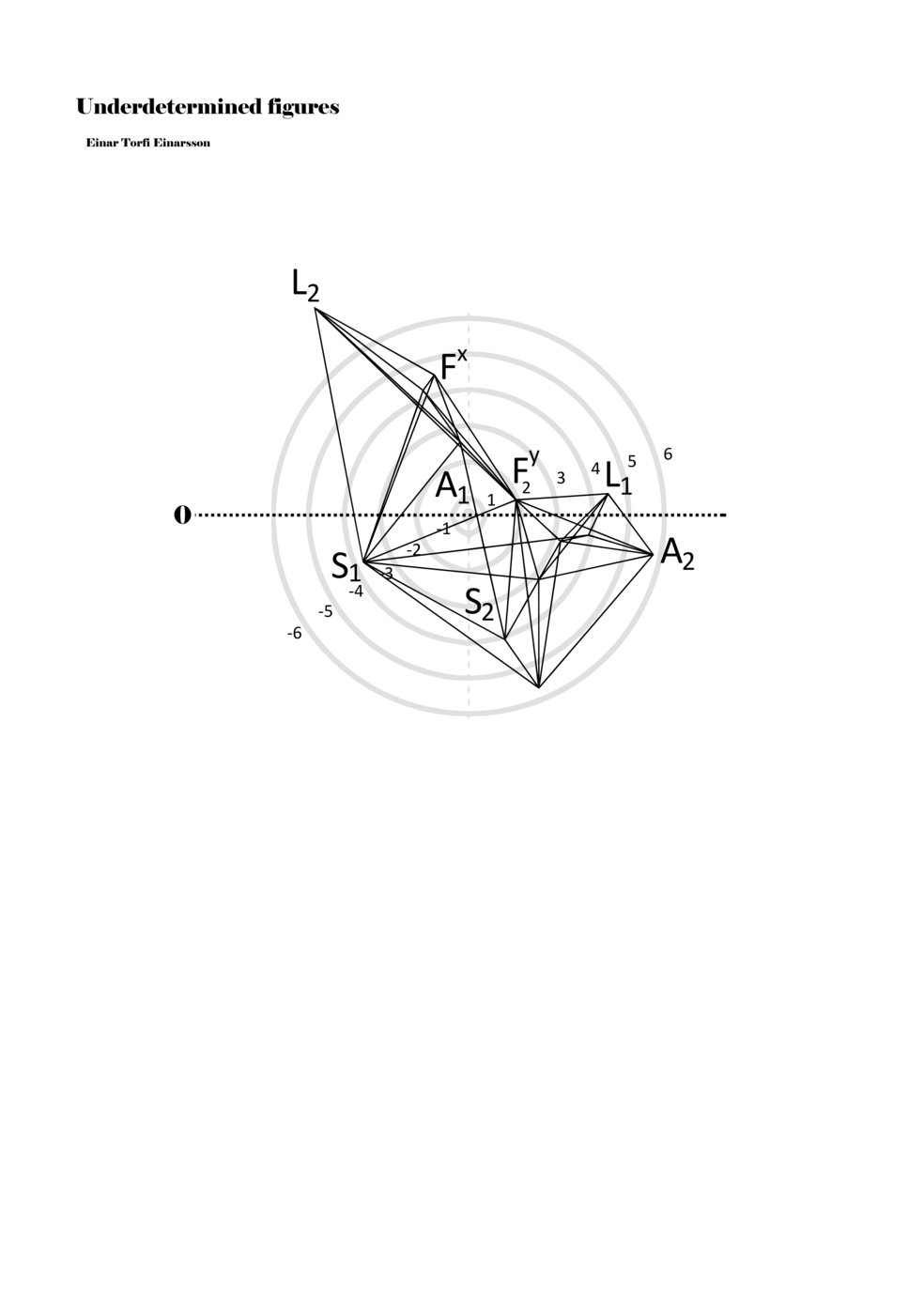
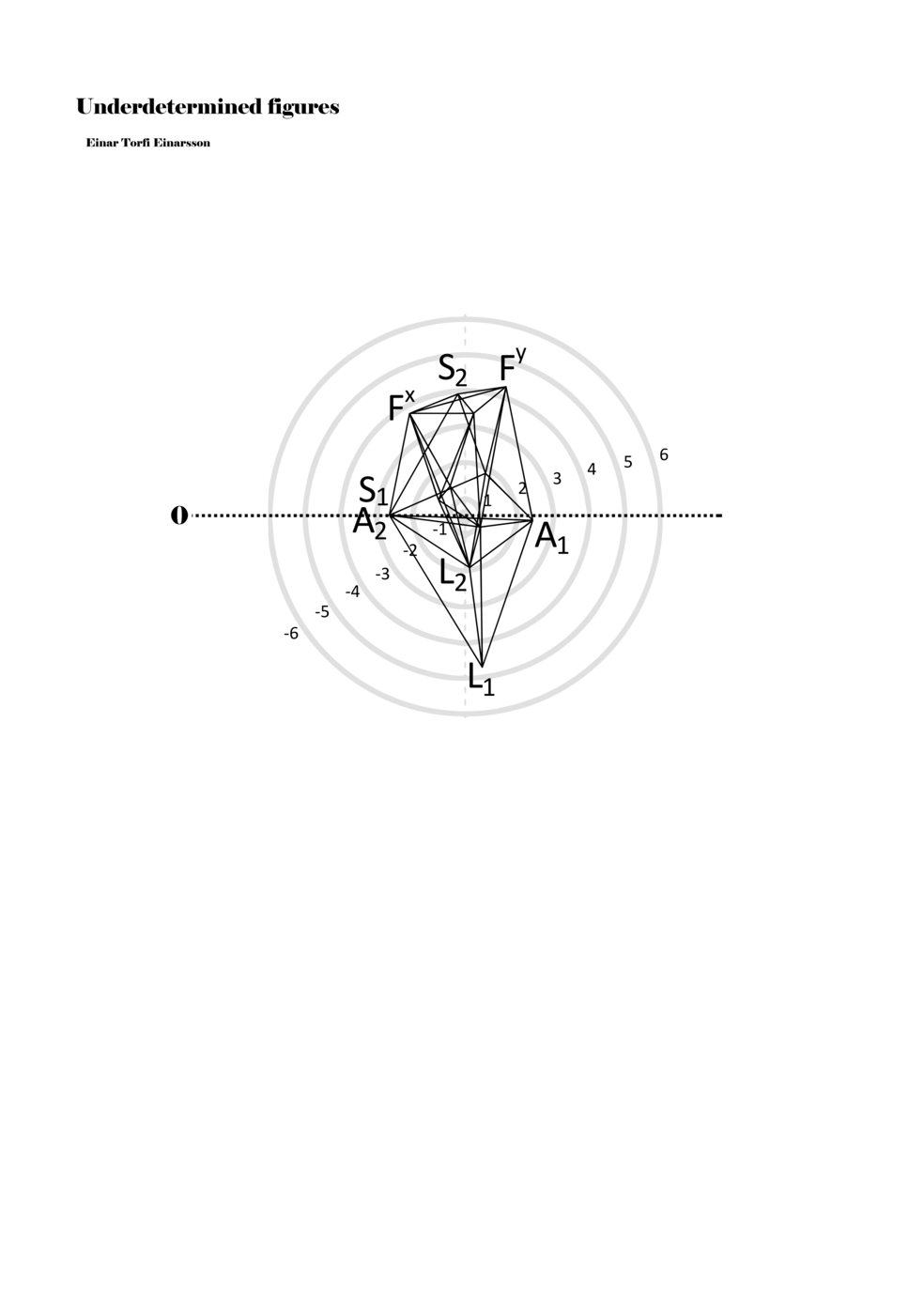
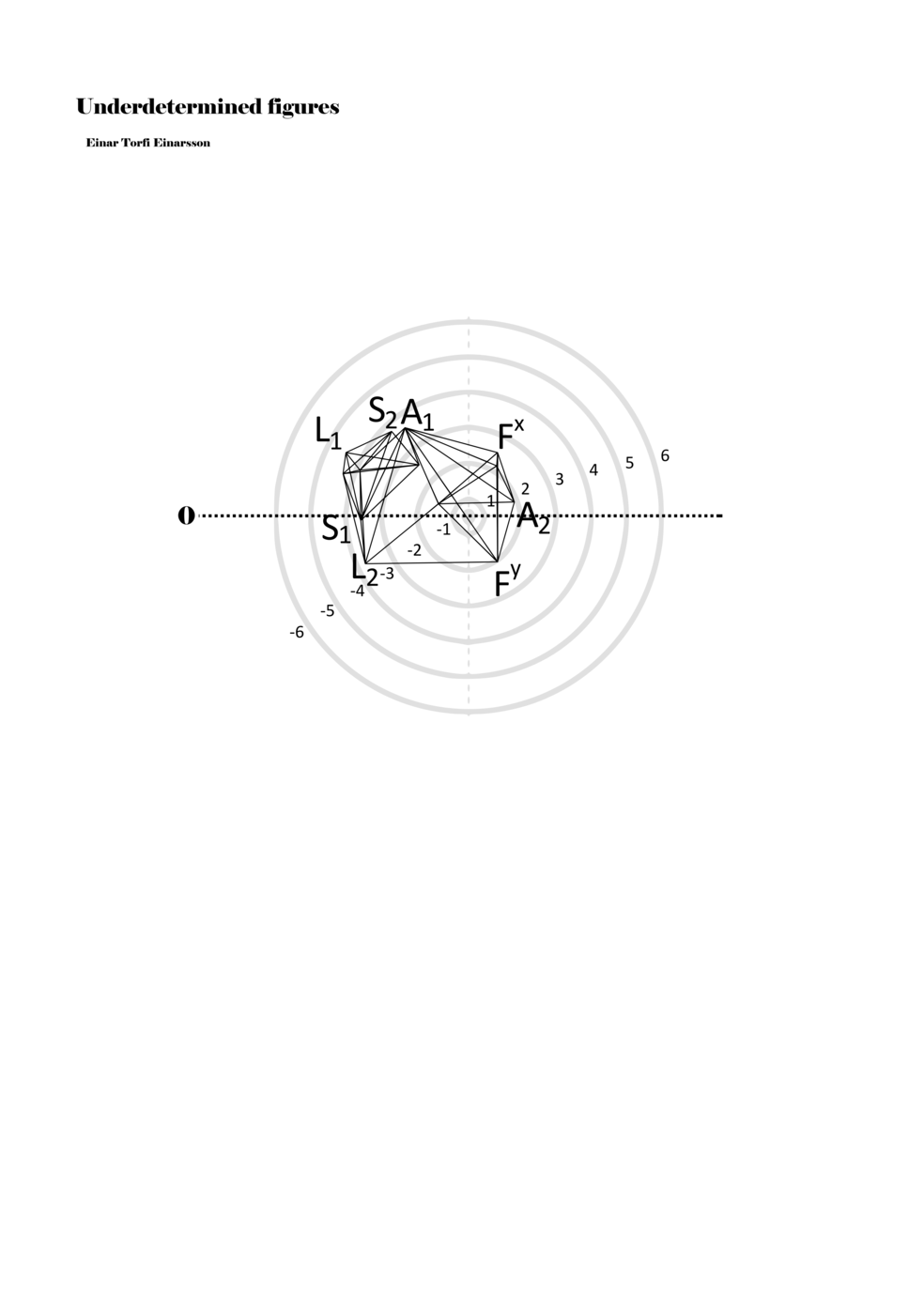
To turn the figures into notations they are placed in a so-called field or parametric space. This field has different circular areas representing numbers from 0 (at the centre) to ±6 (outermost). Because of this construction, a line that crosses the so-called null line (splitting the circles in half at the centre) can result in a nonlinear parametric jump. For example, the line in example 1 is between two points, +5 and -3, but its path results in a nonlinear relationship between the points: 5, 4, -4, -3 (i.e., a jump happens from 4 to -4). Furthermore, although the difference between positive and negative numbers varies between parameters, in general, negative numbers indicate how the performer approaches an action both mentally (imagining it) and physically (movement of hands and fingers close to the instrument) while positive numbers indicate action on the instrument (e.g., where and how the instrument is played).      

Example 1. Contextual notational field or the parametric space

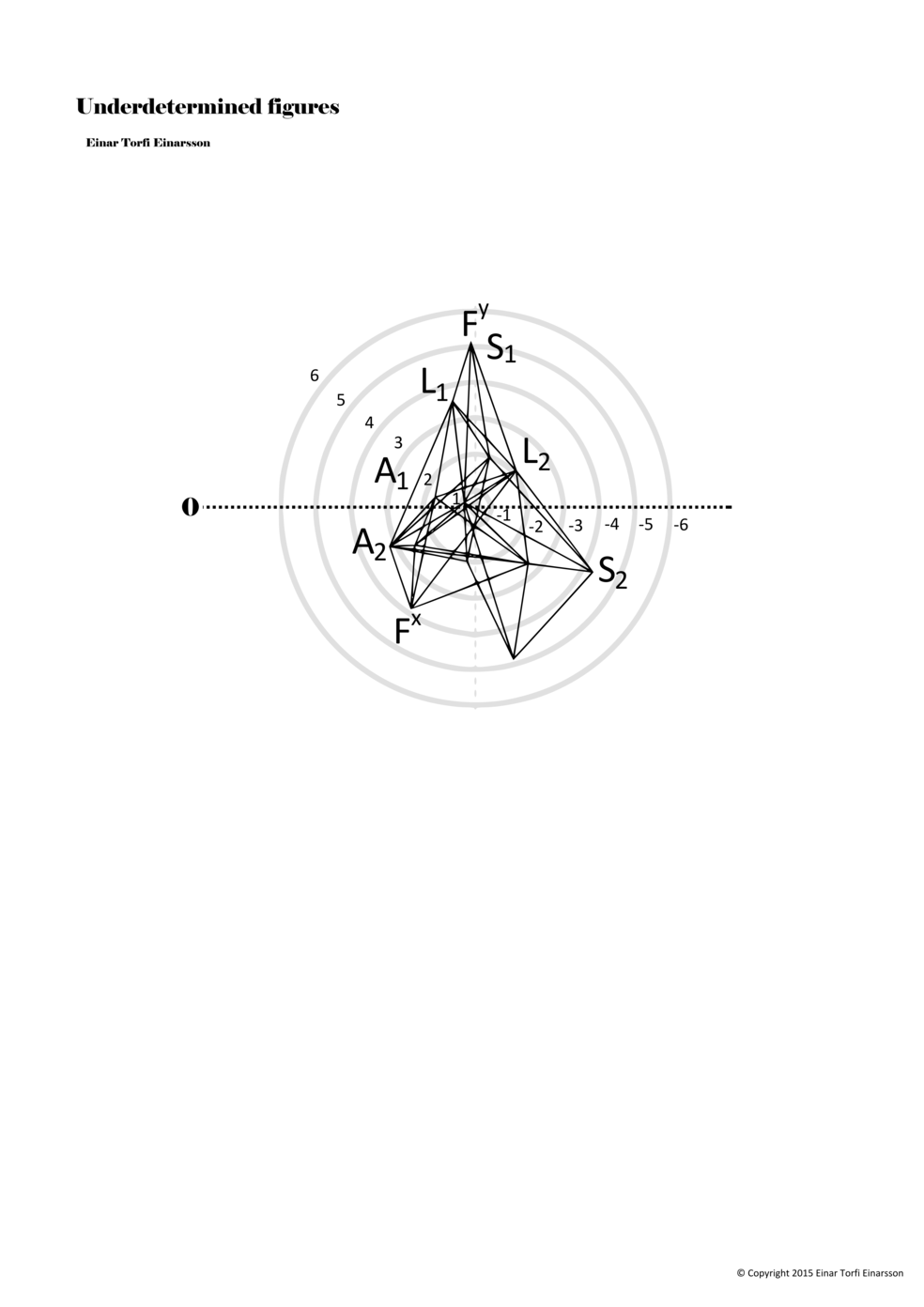
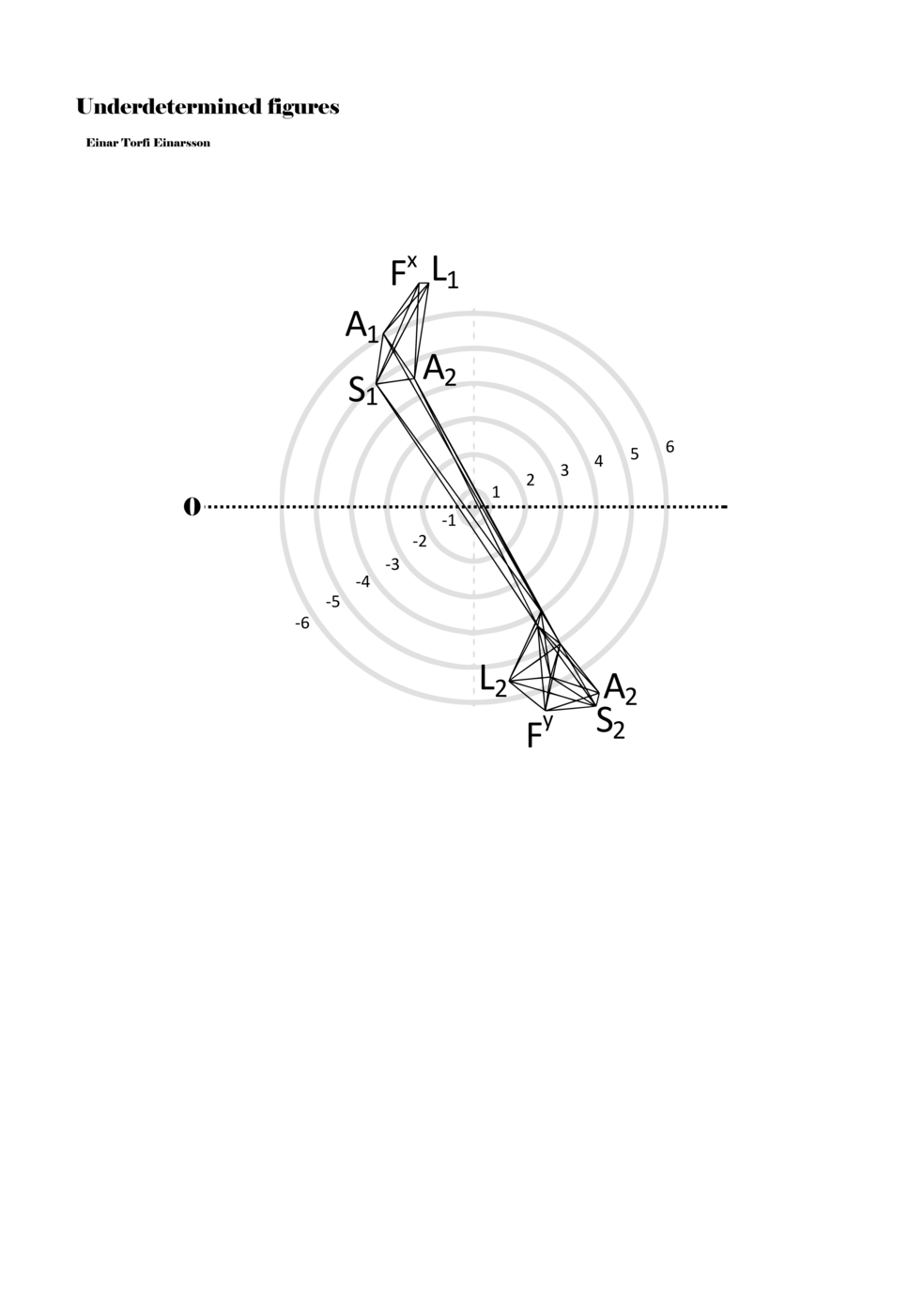
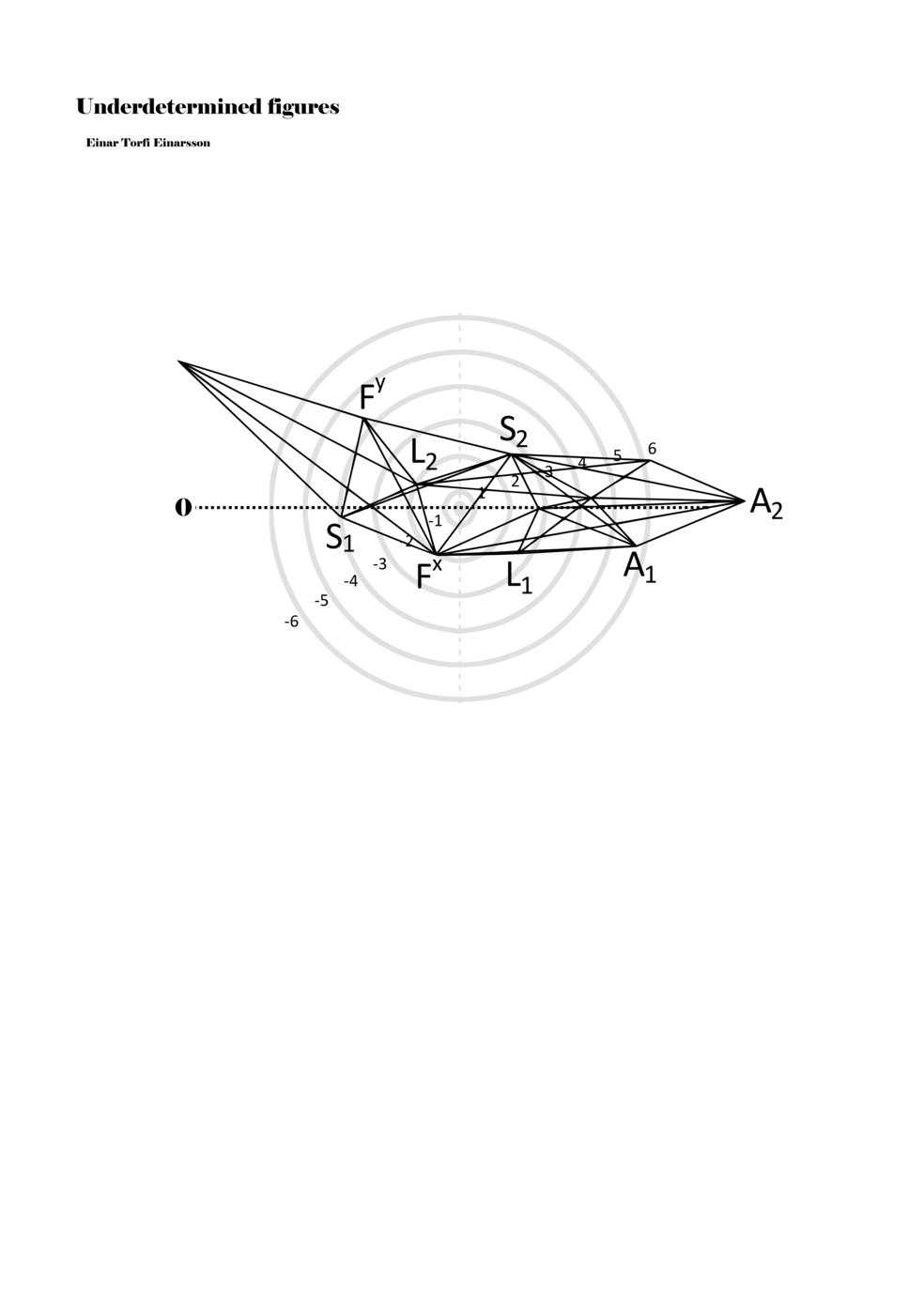
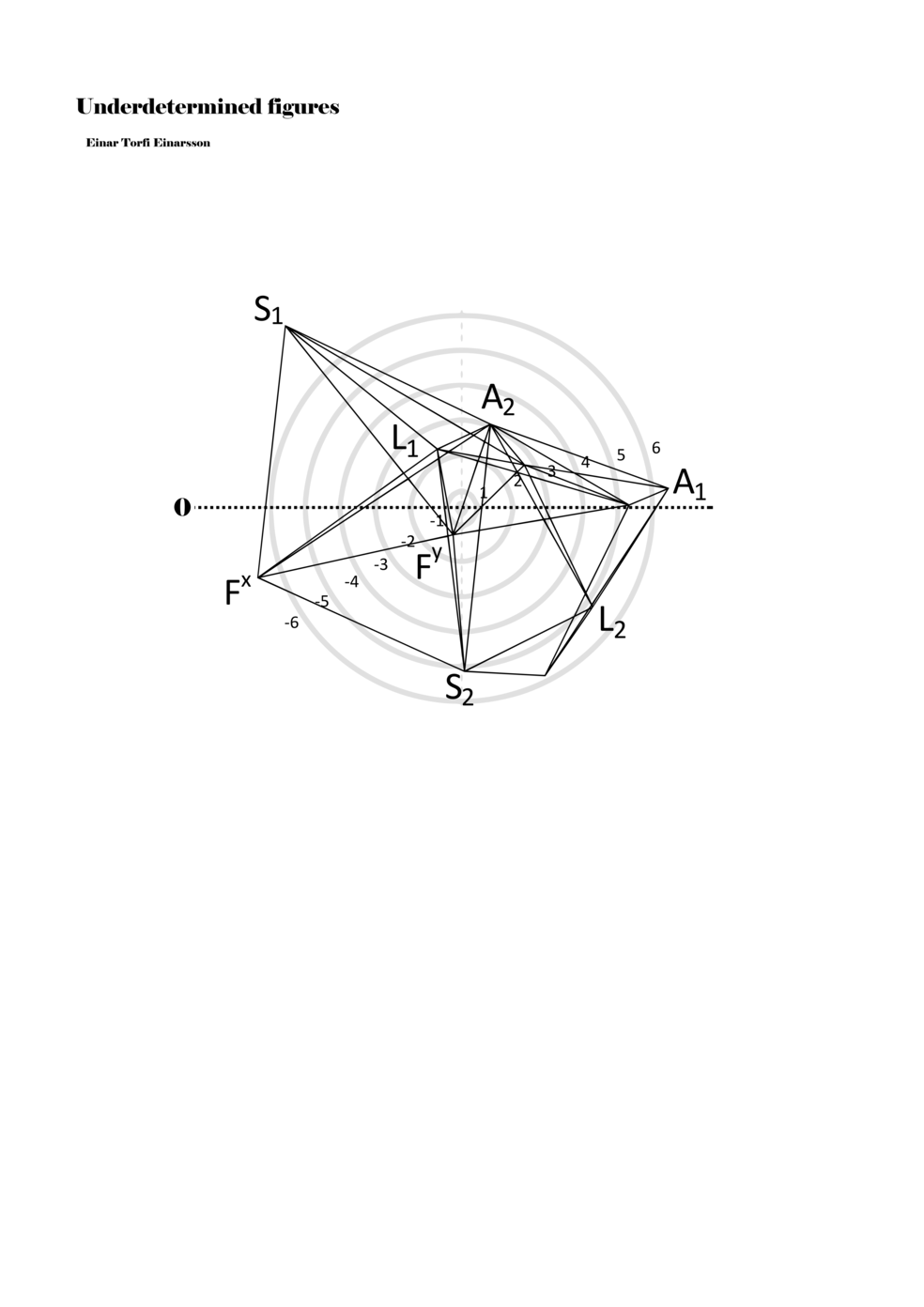
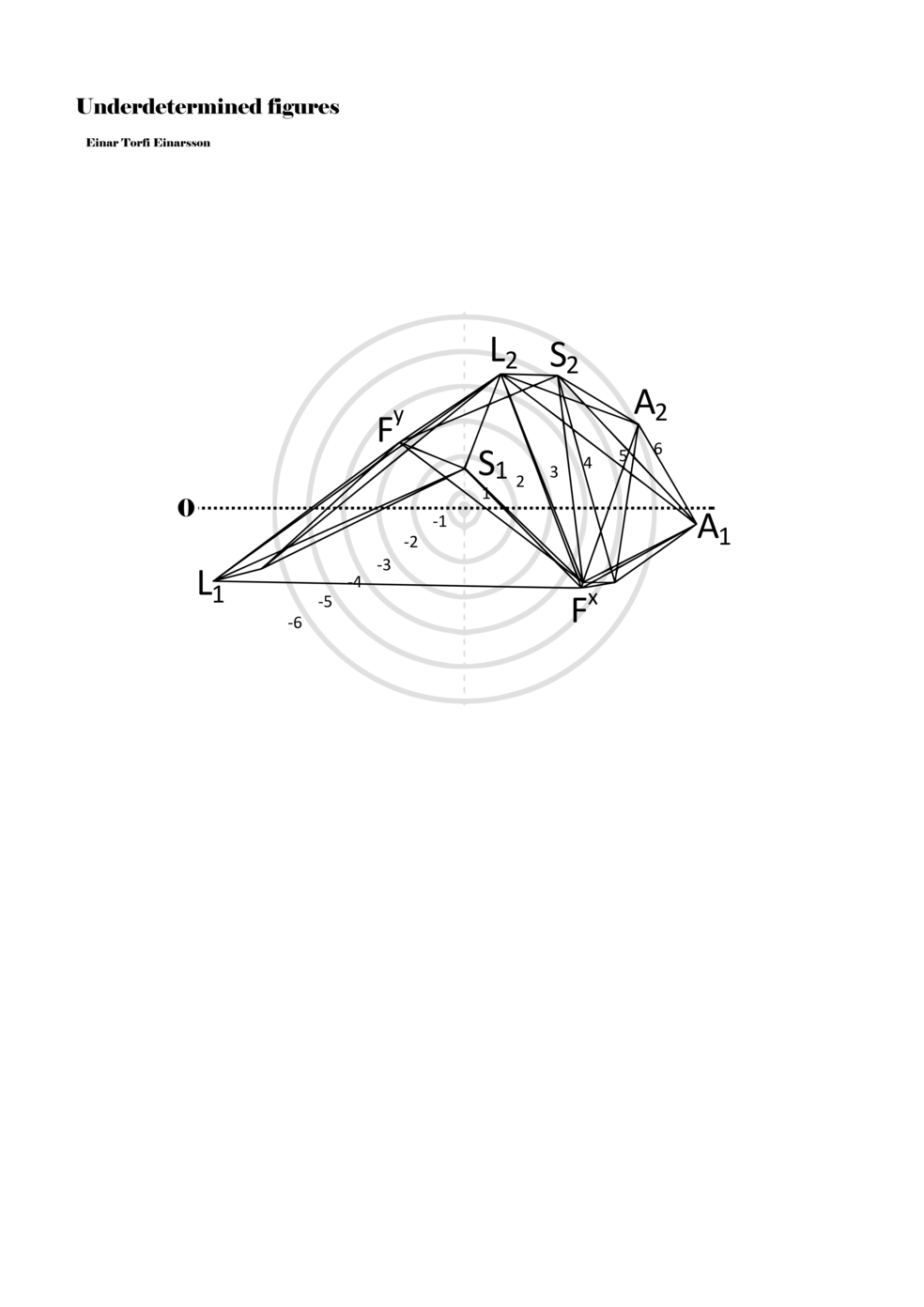
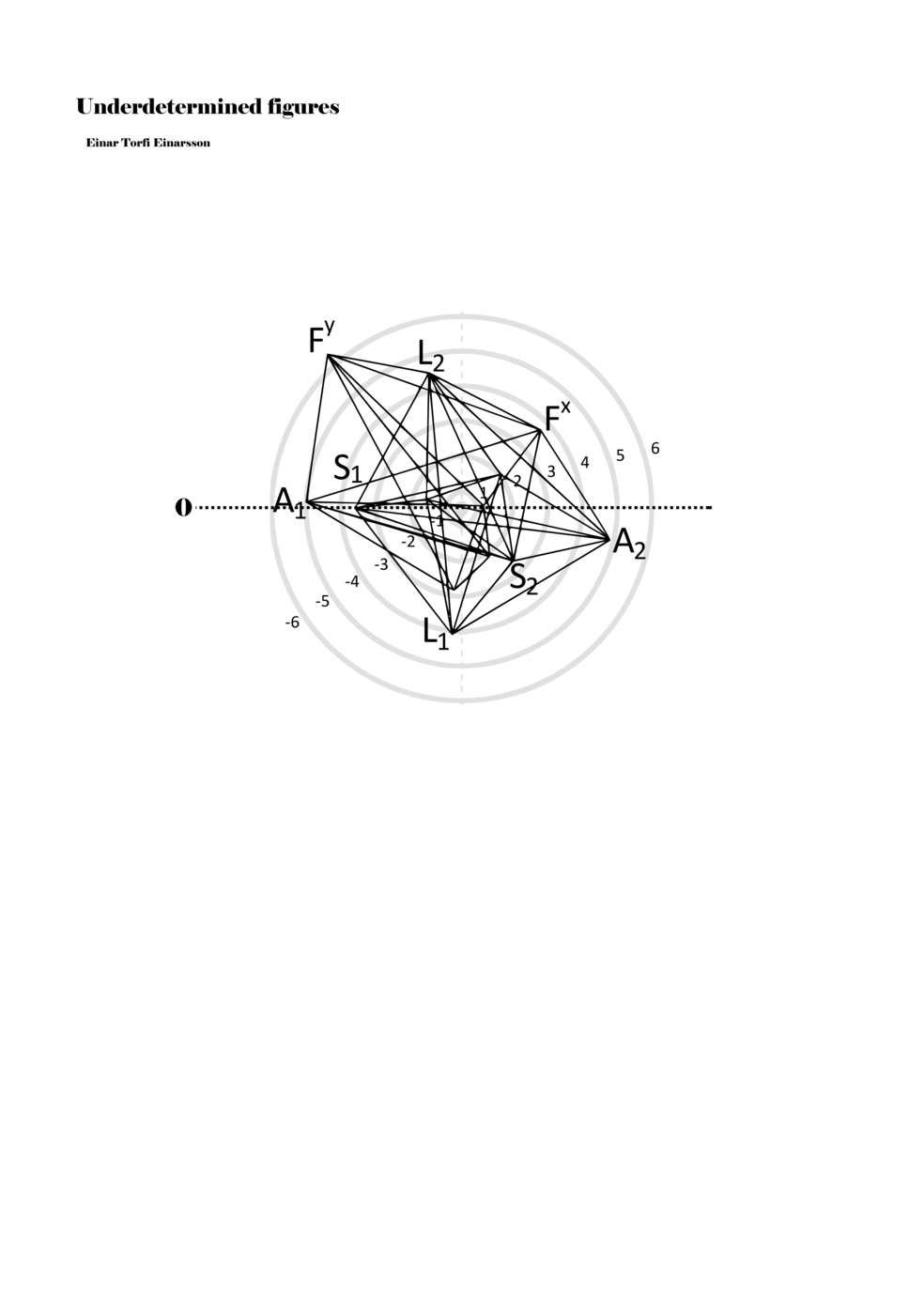
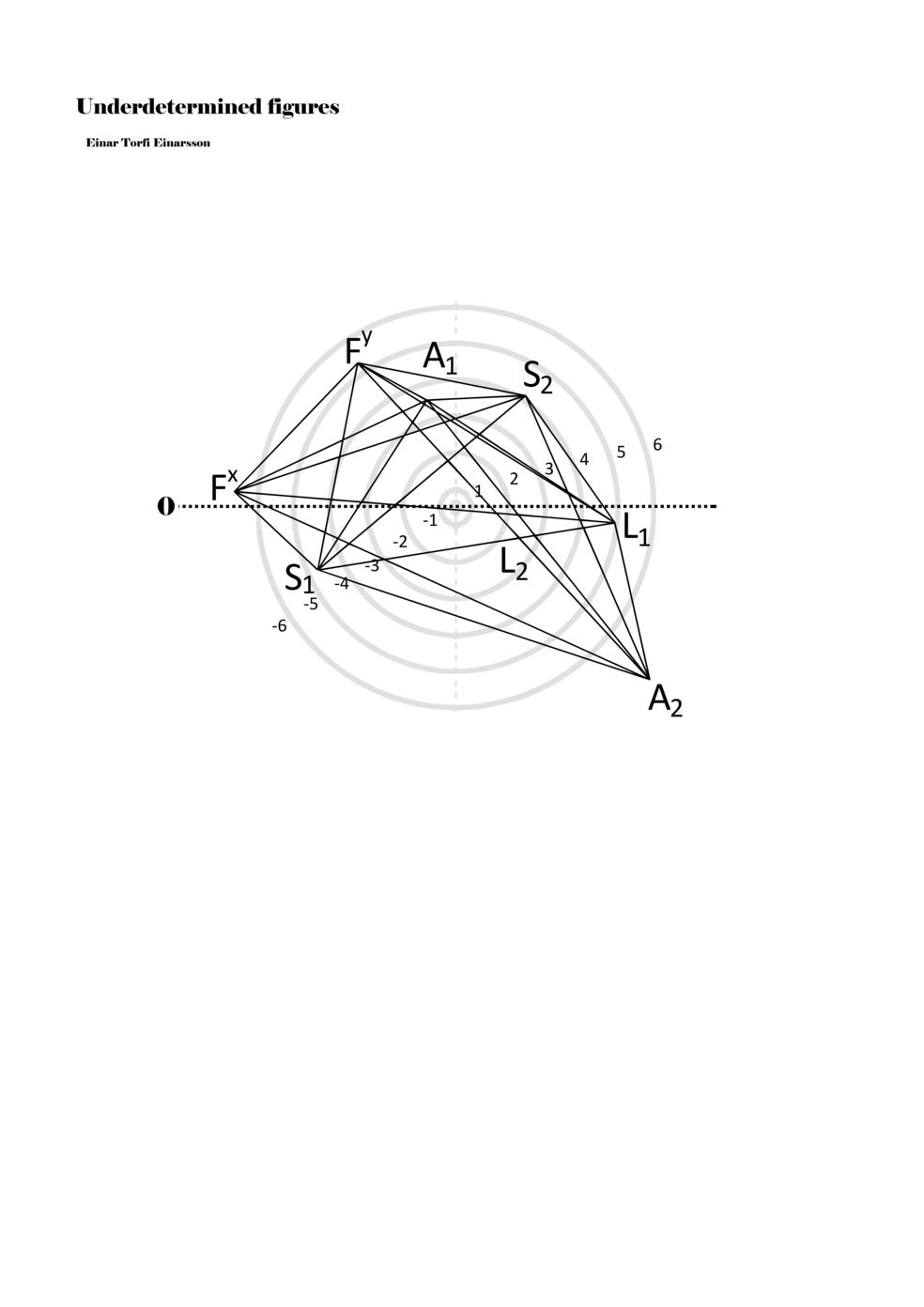
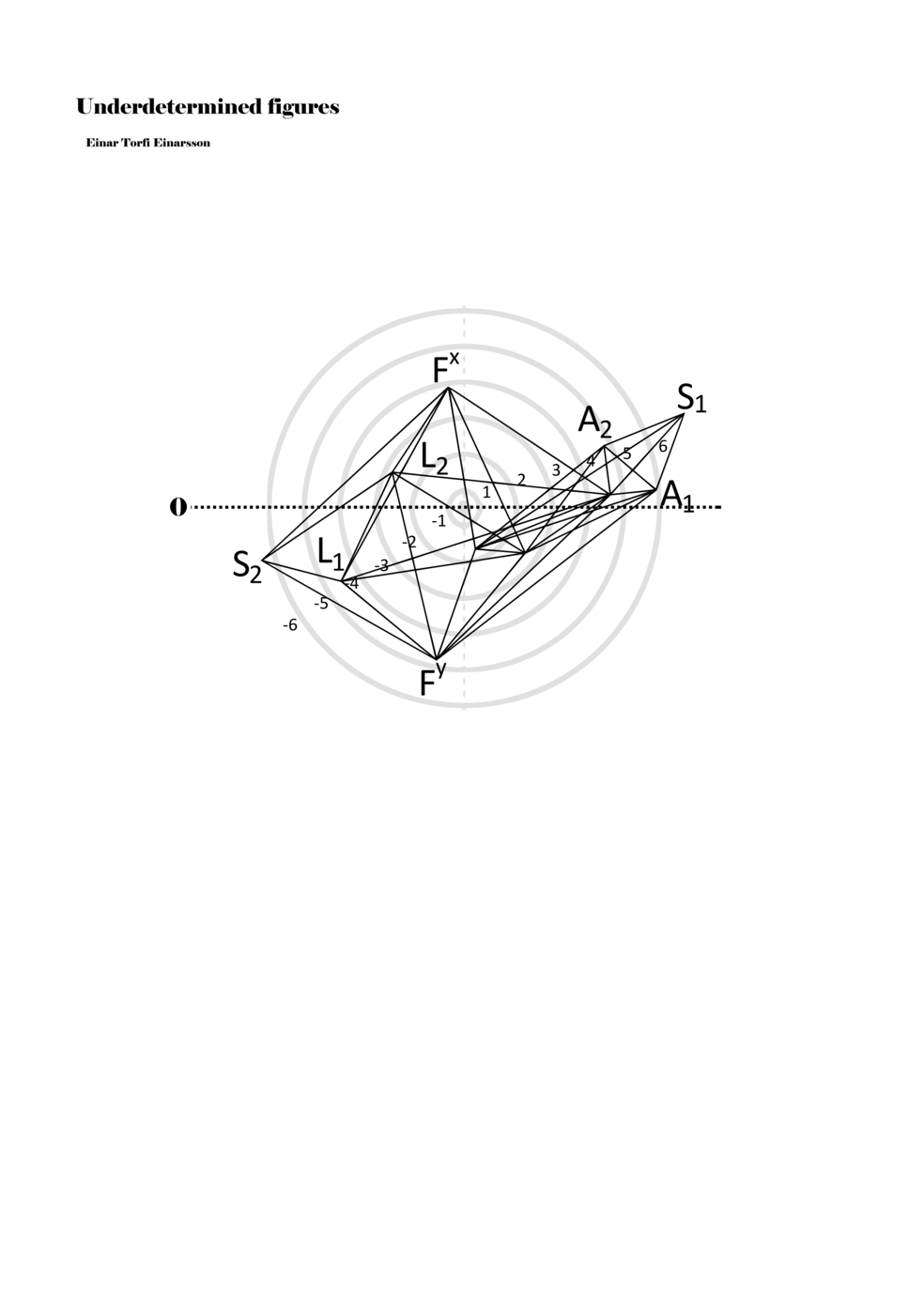
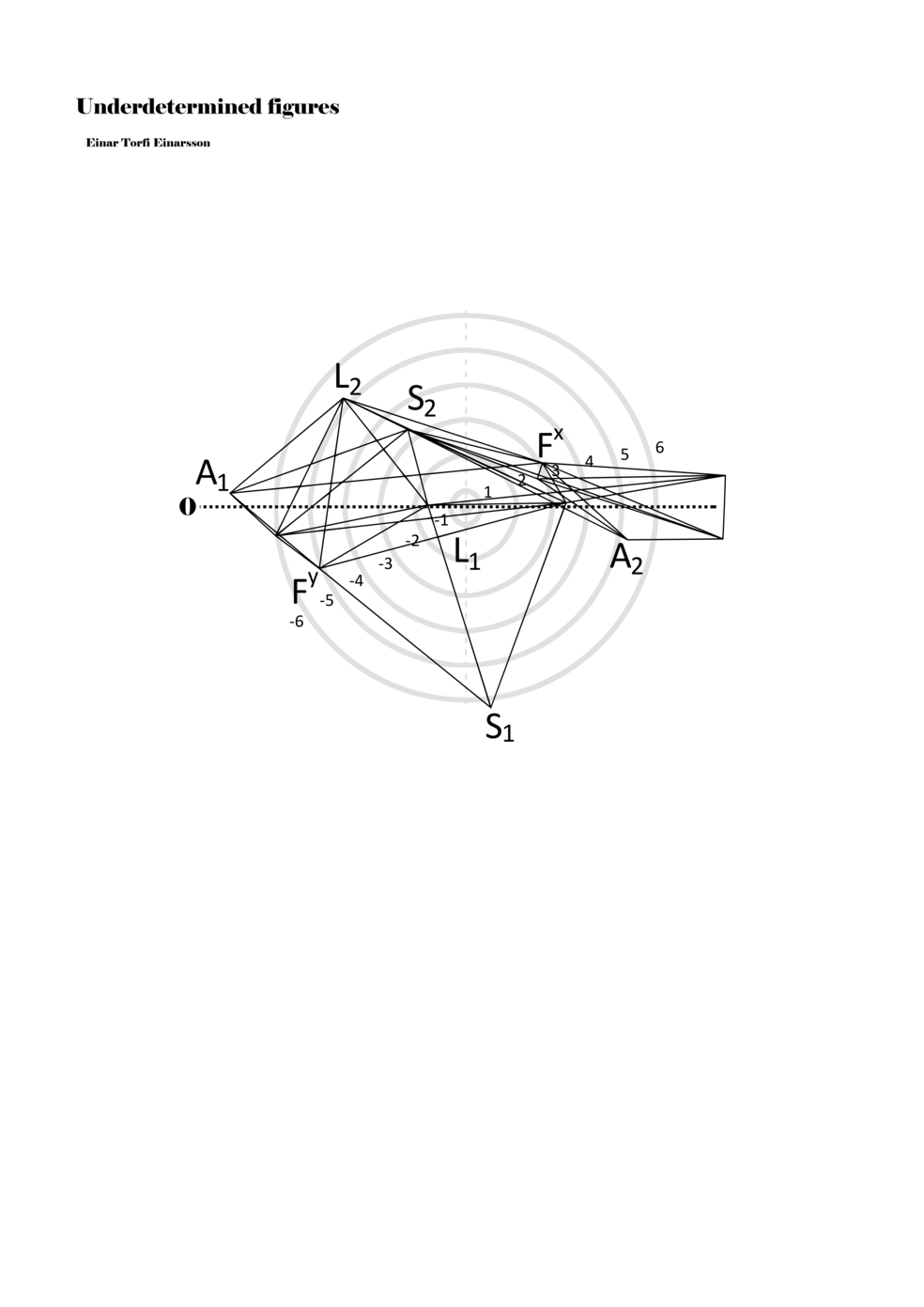
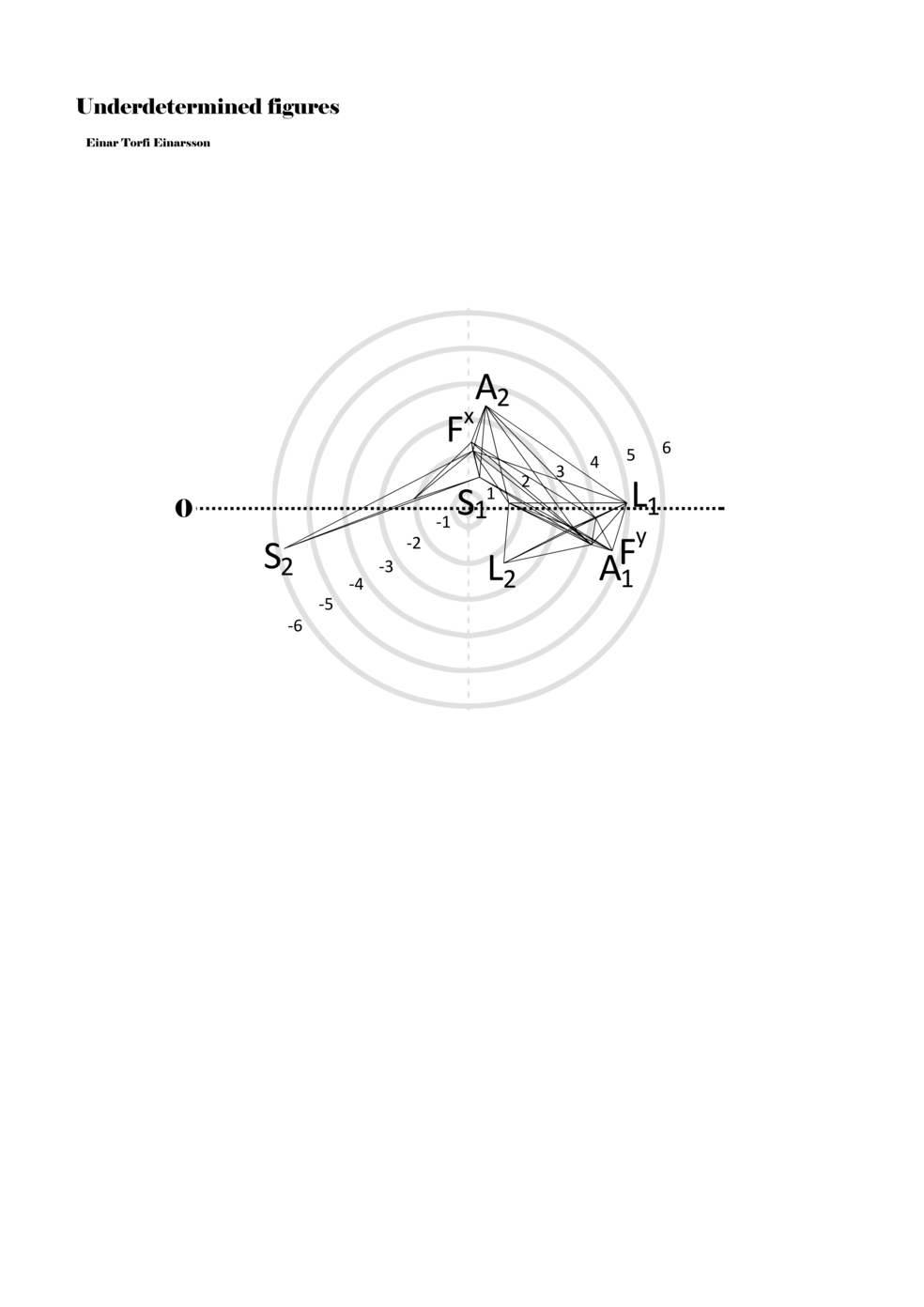
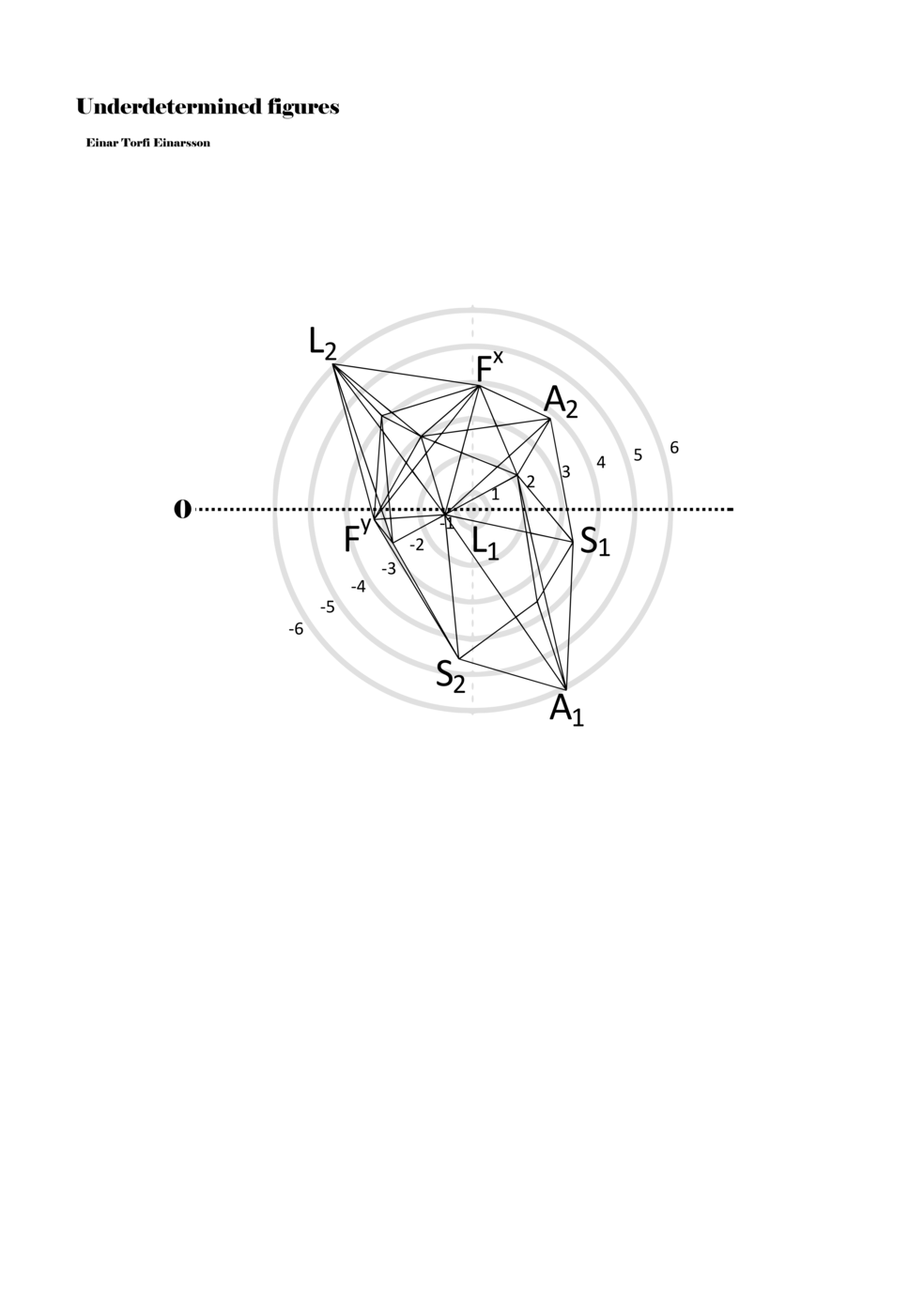
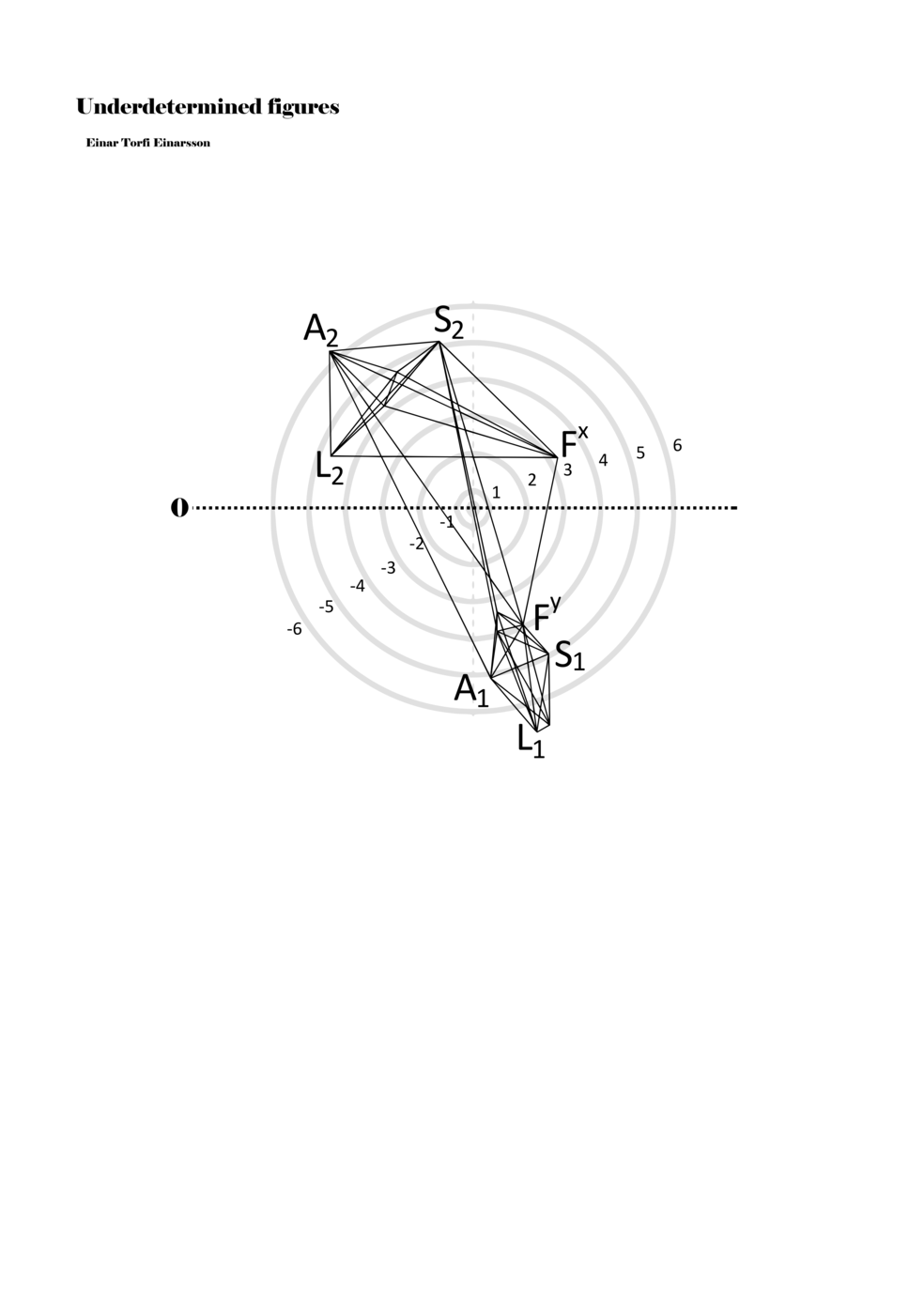
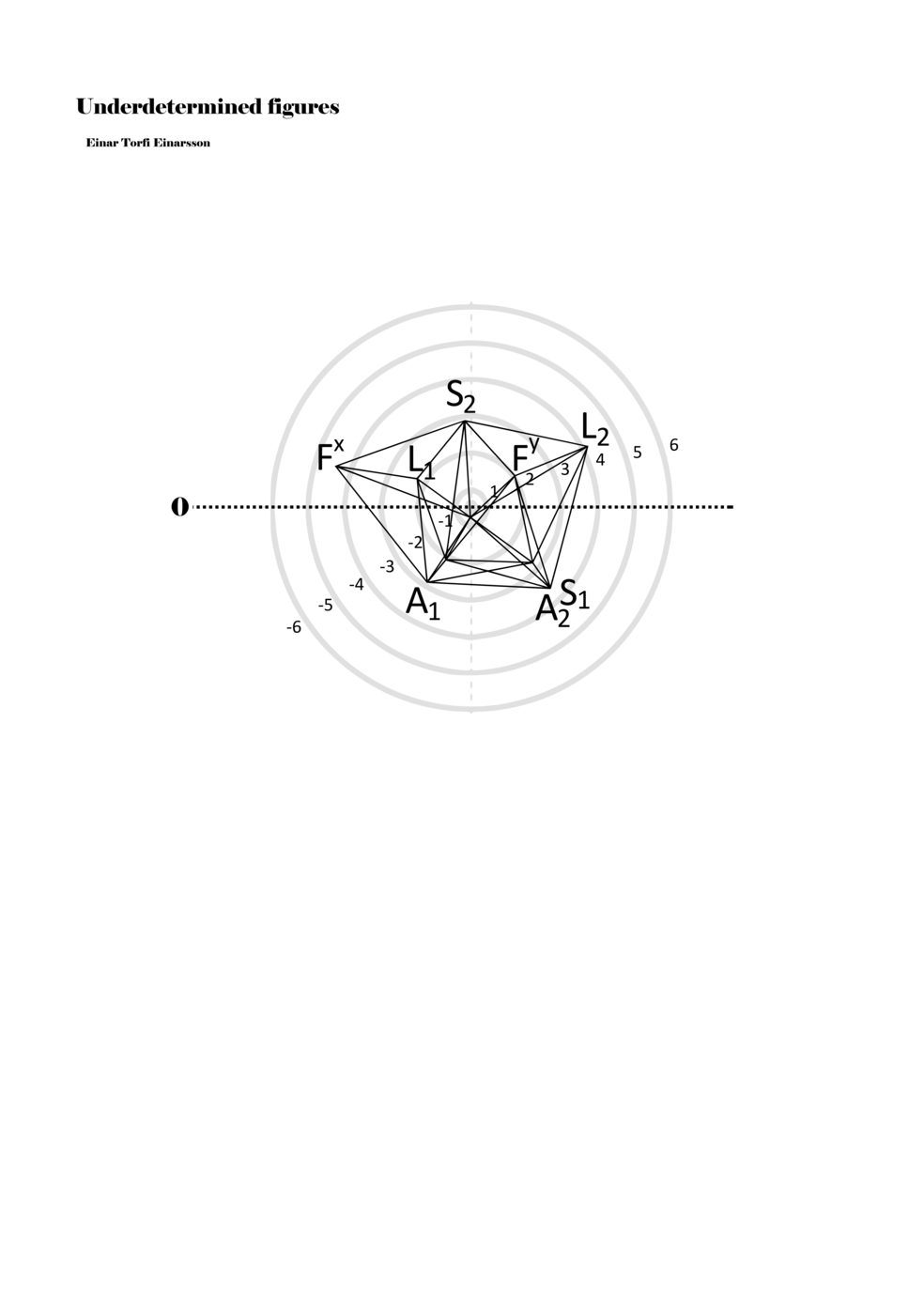
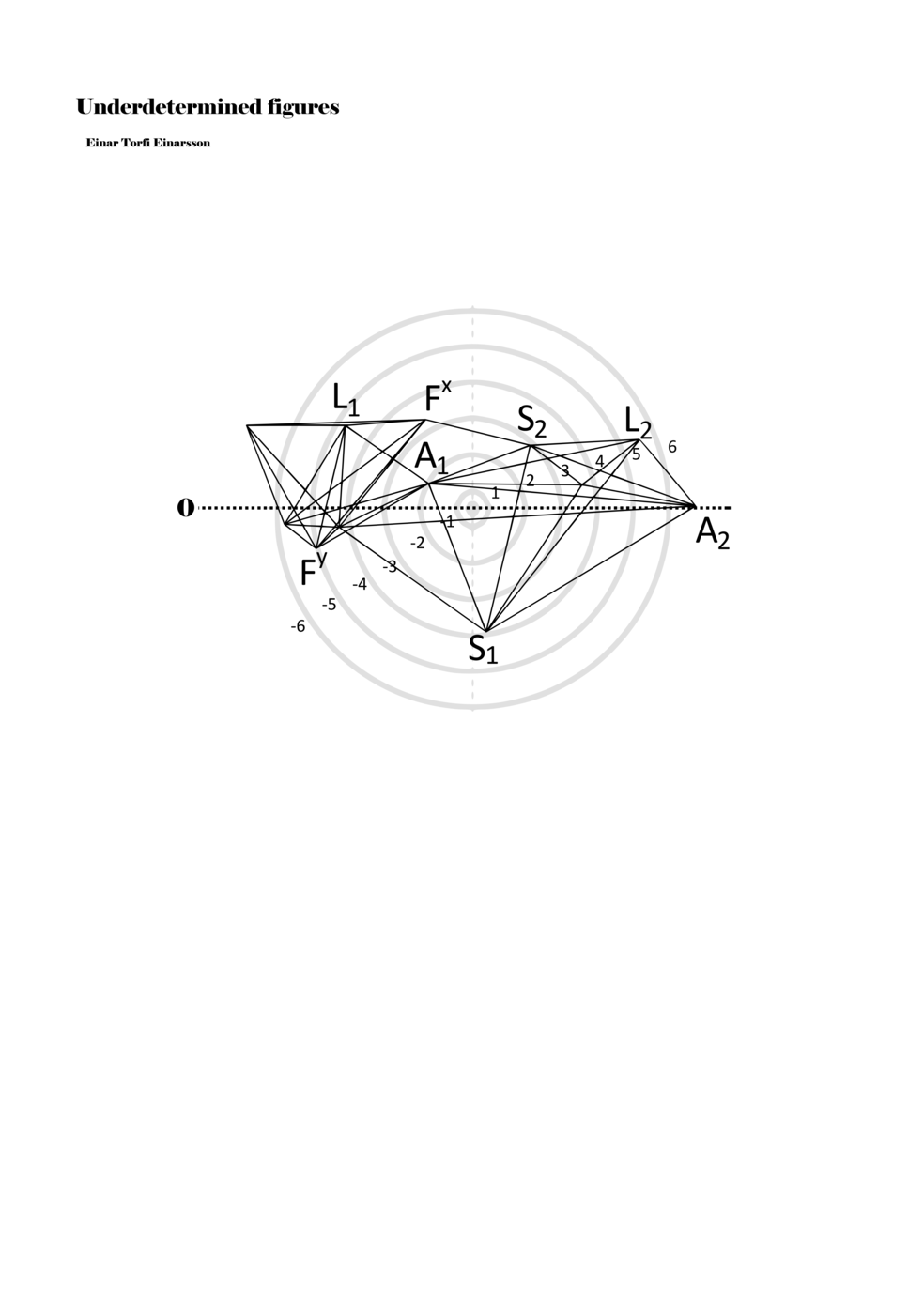
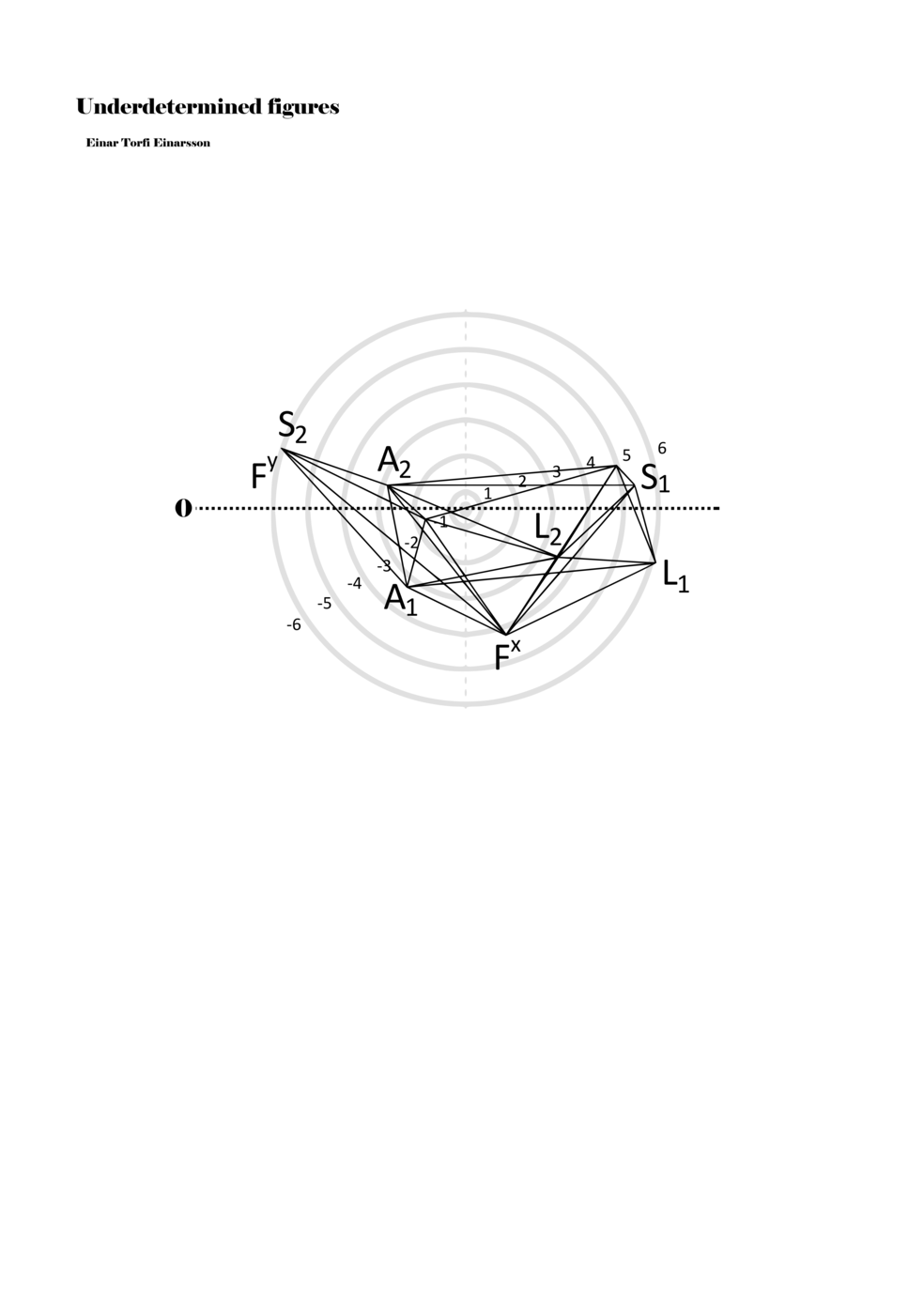
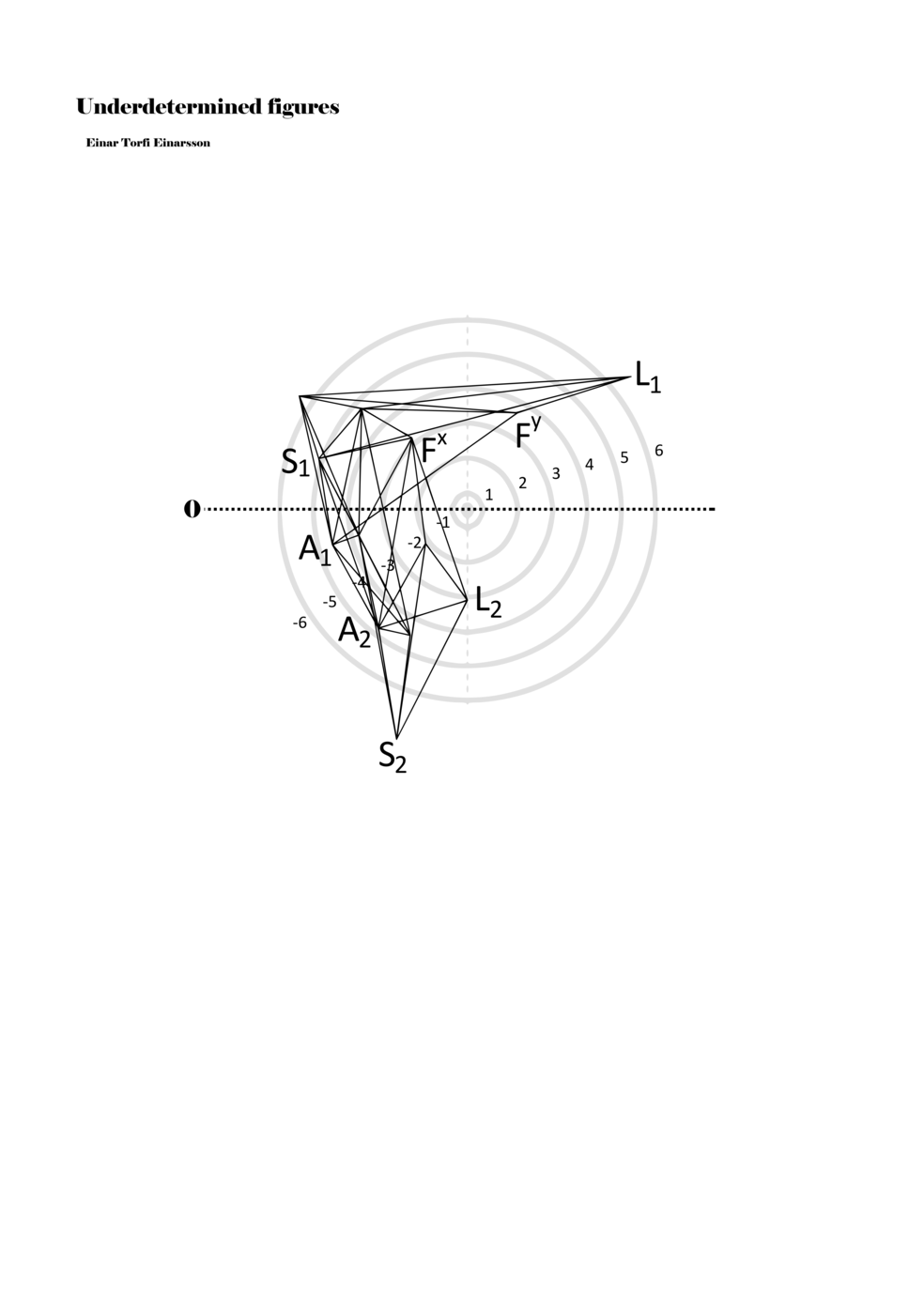
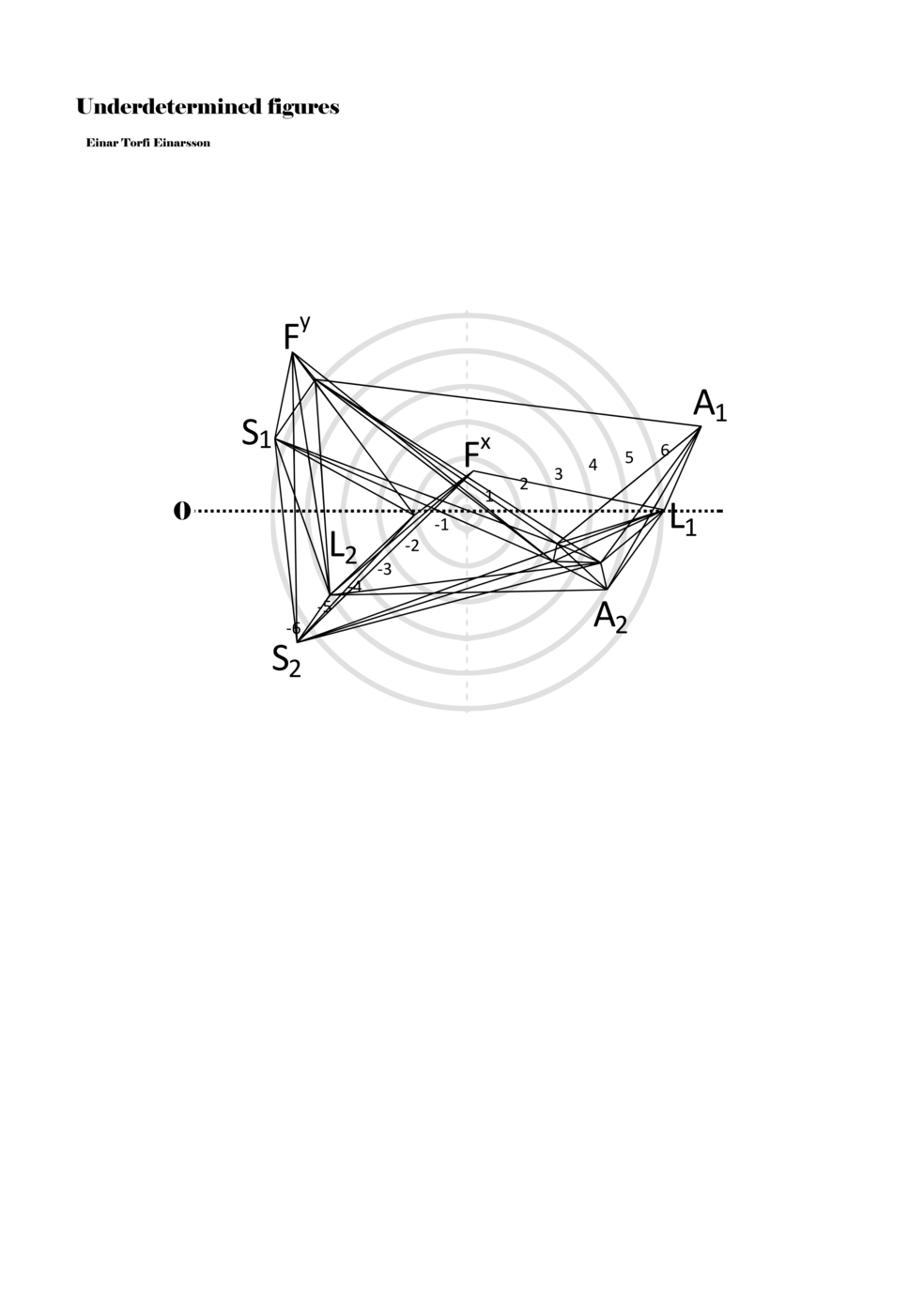
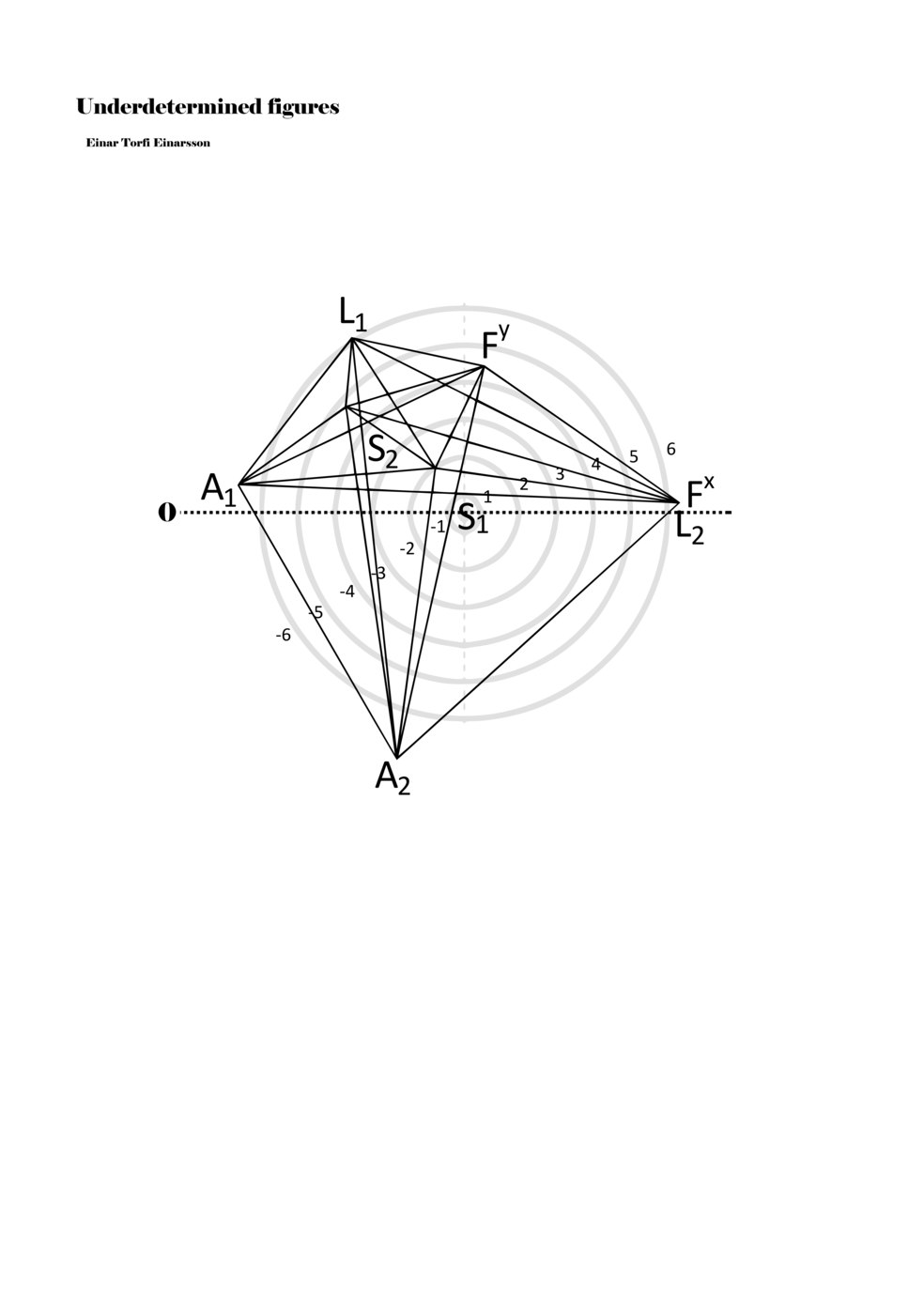
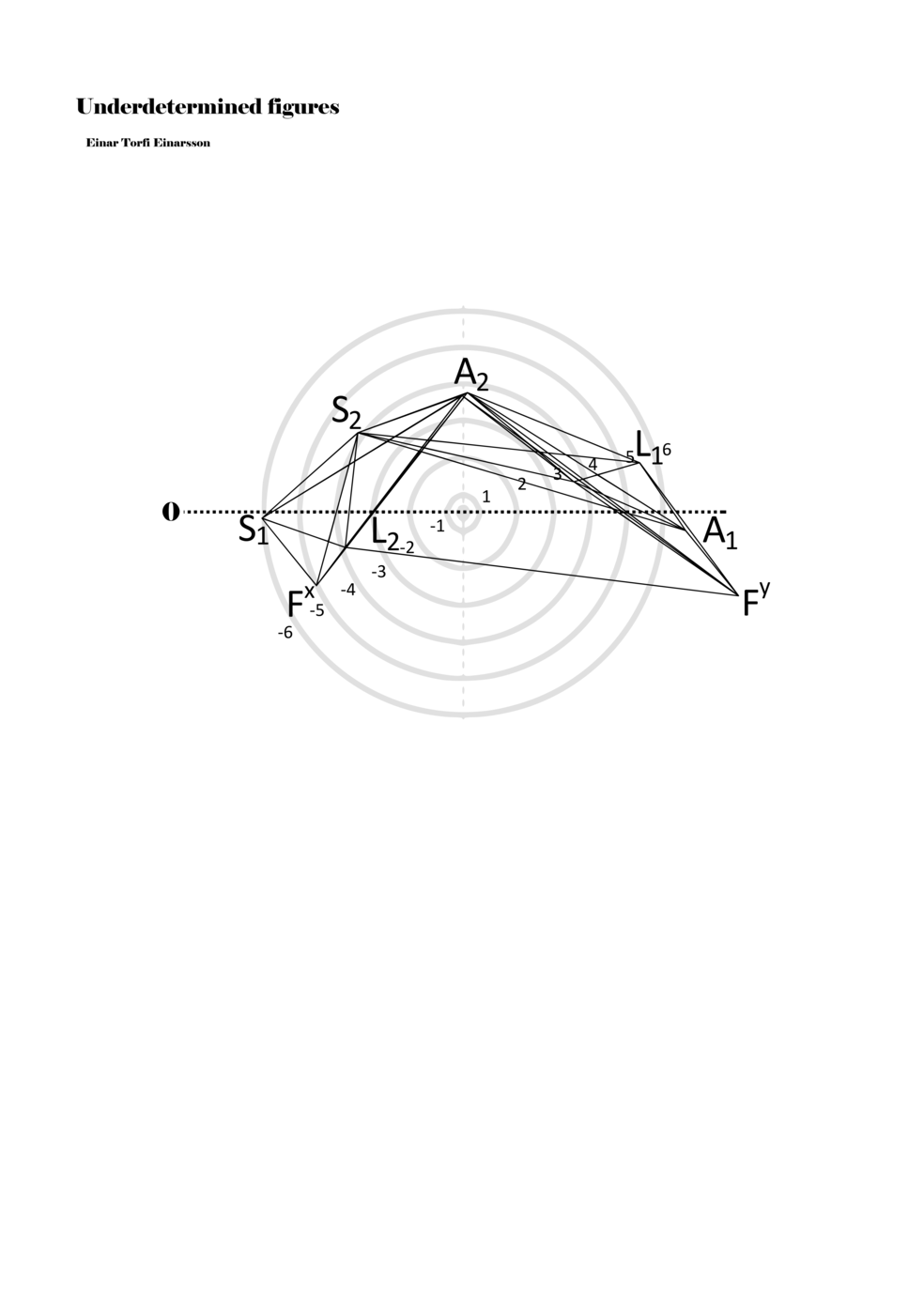
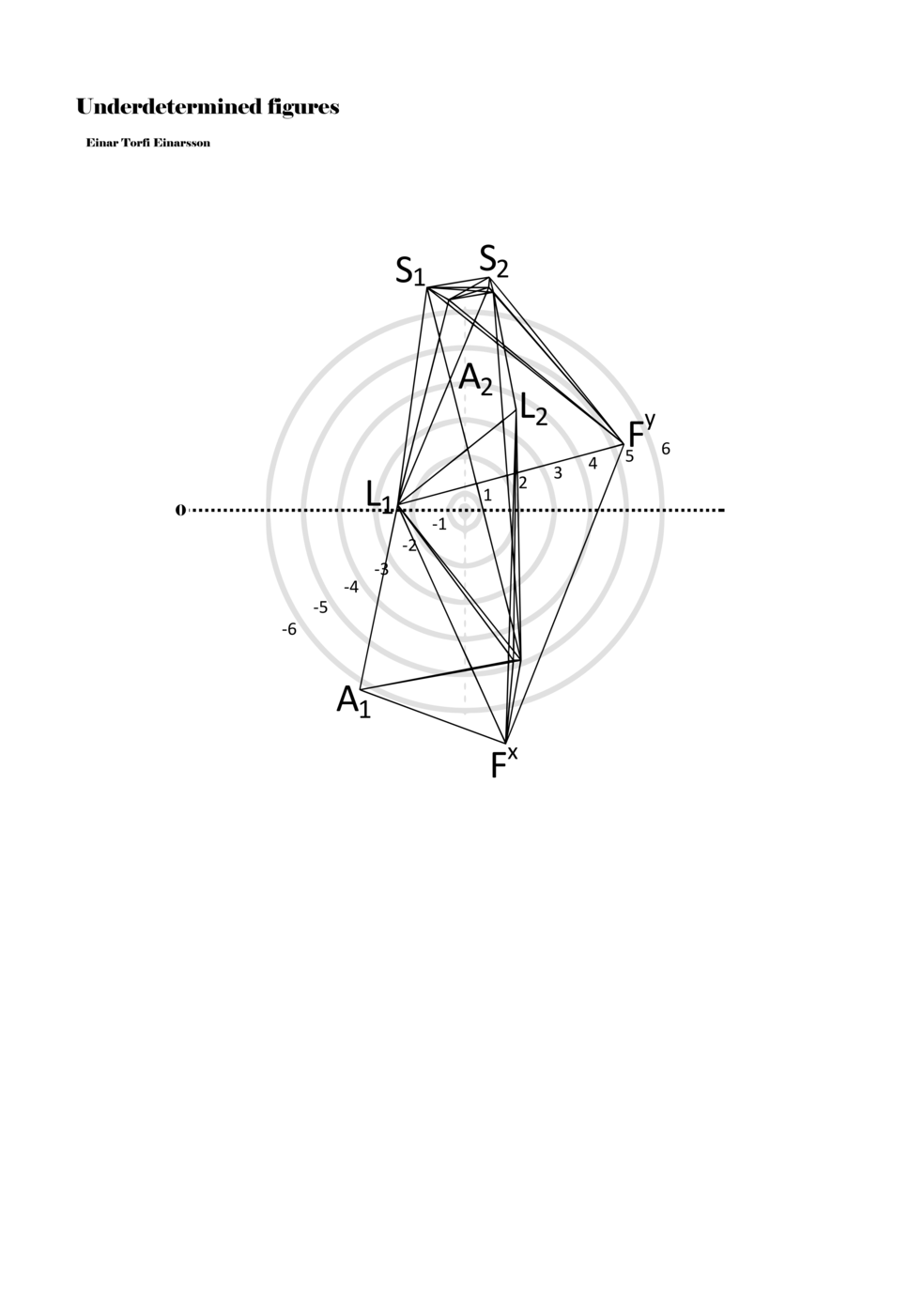
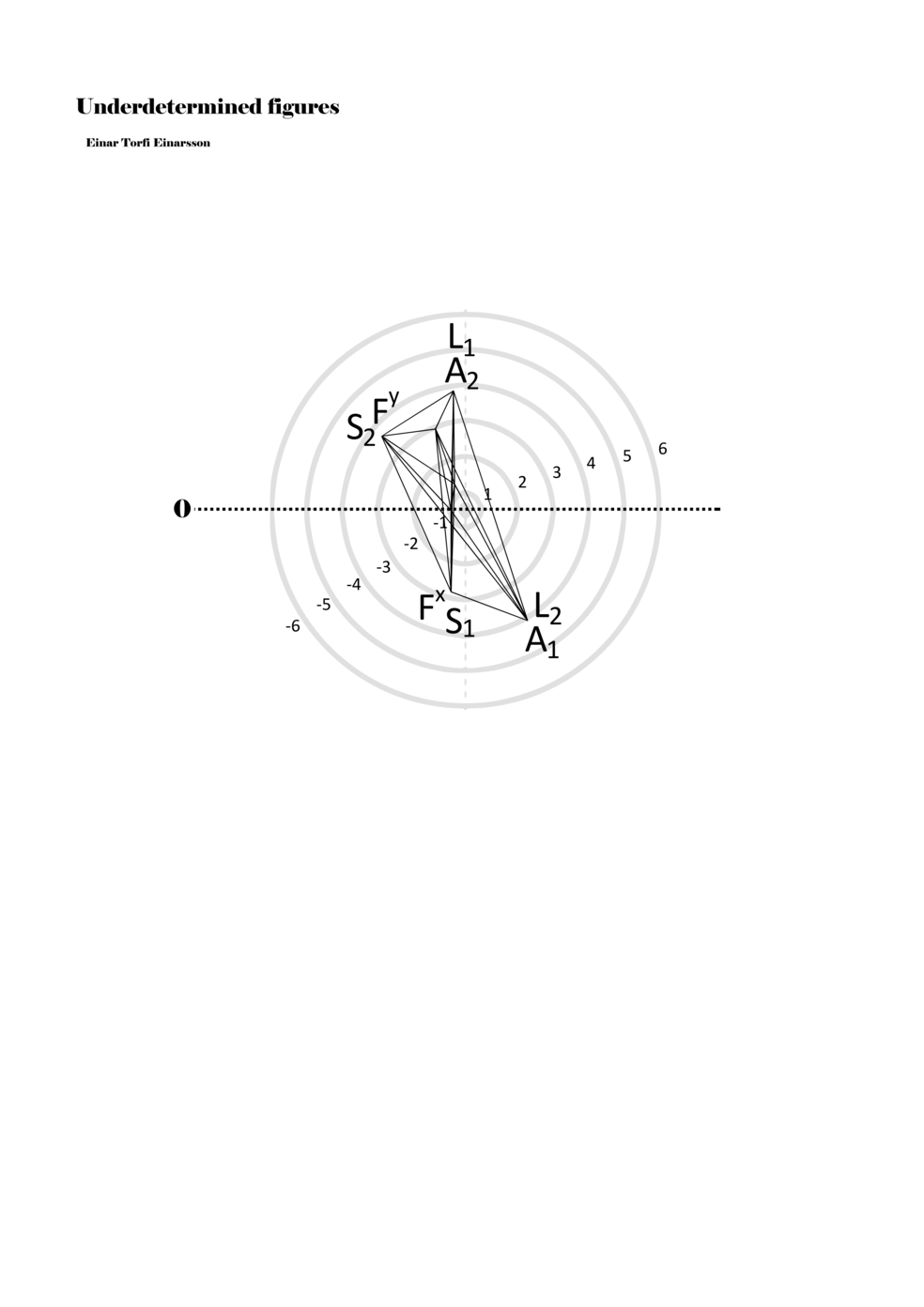
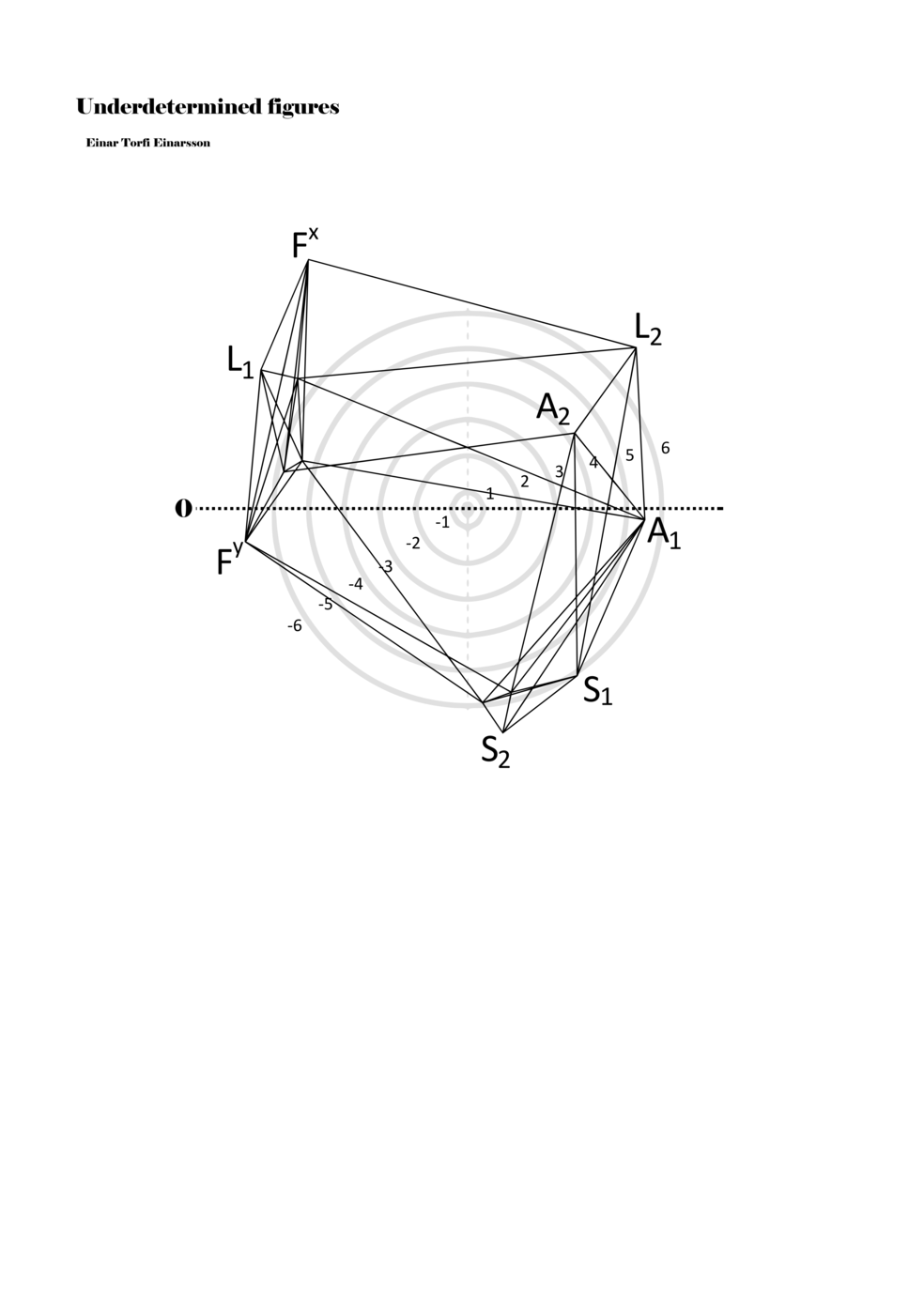
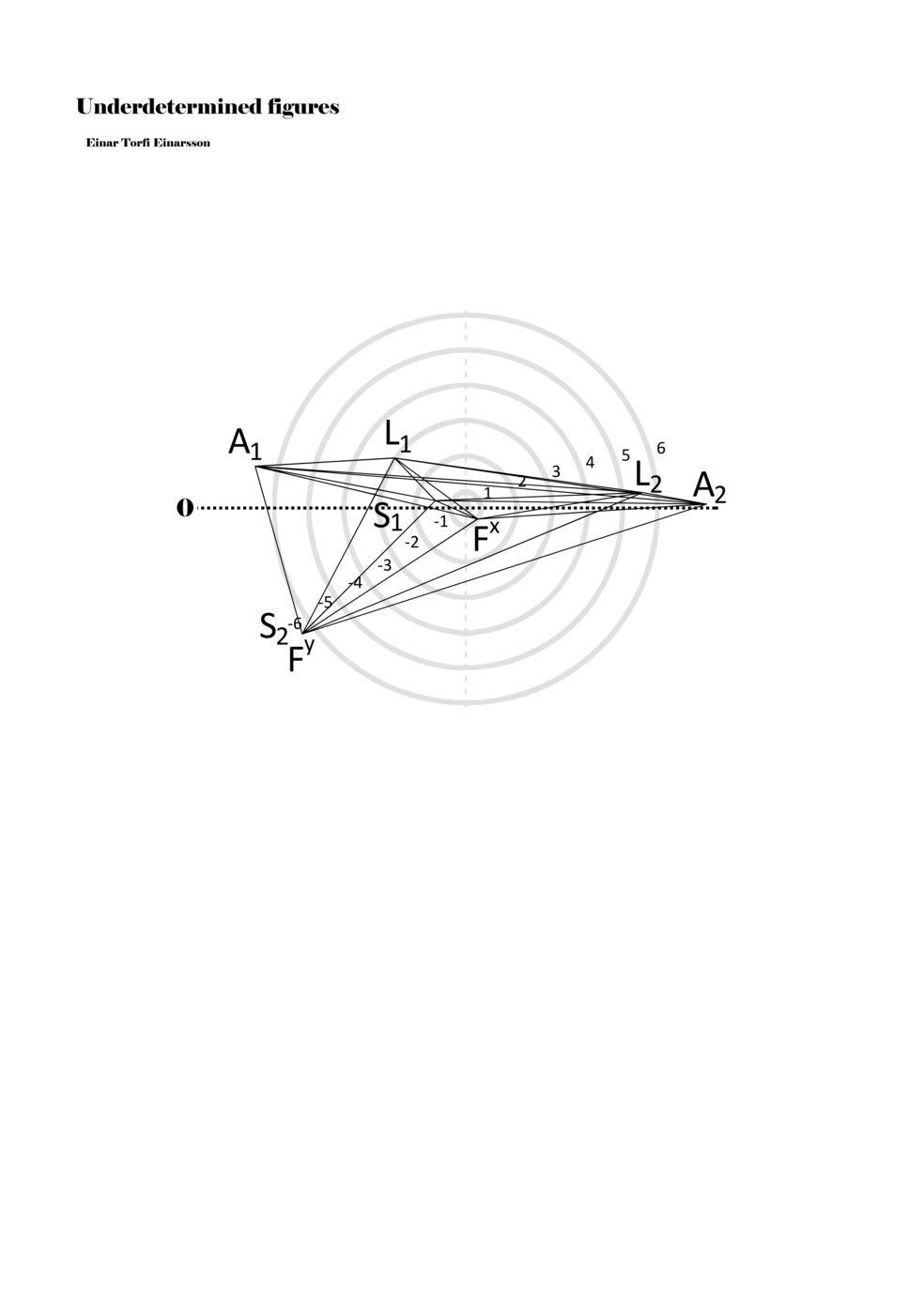
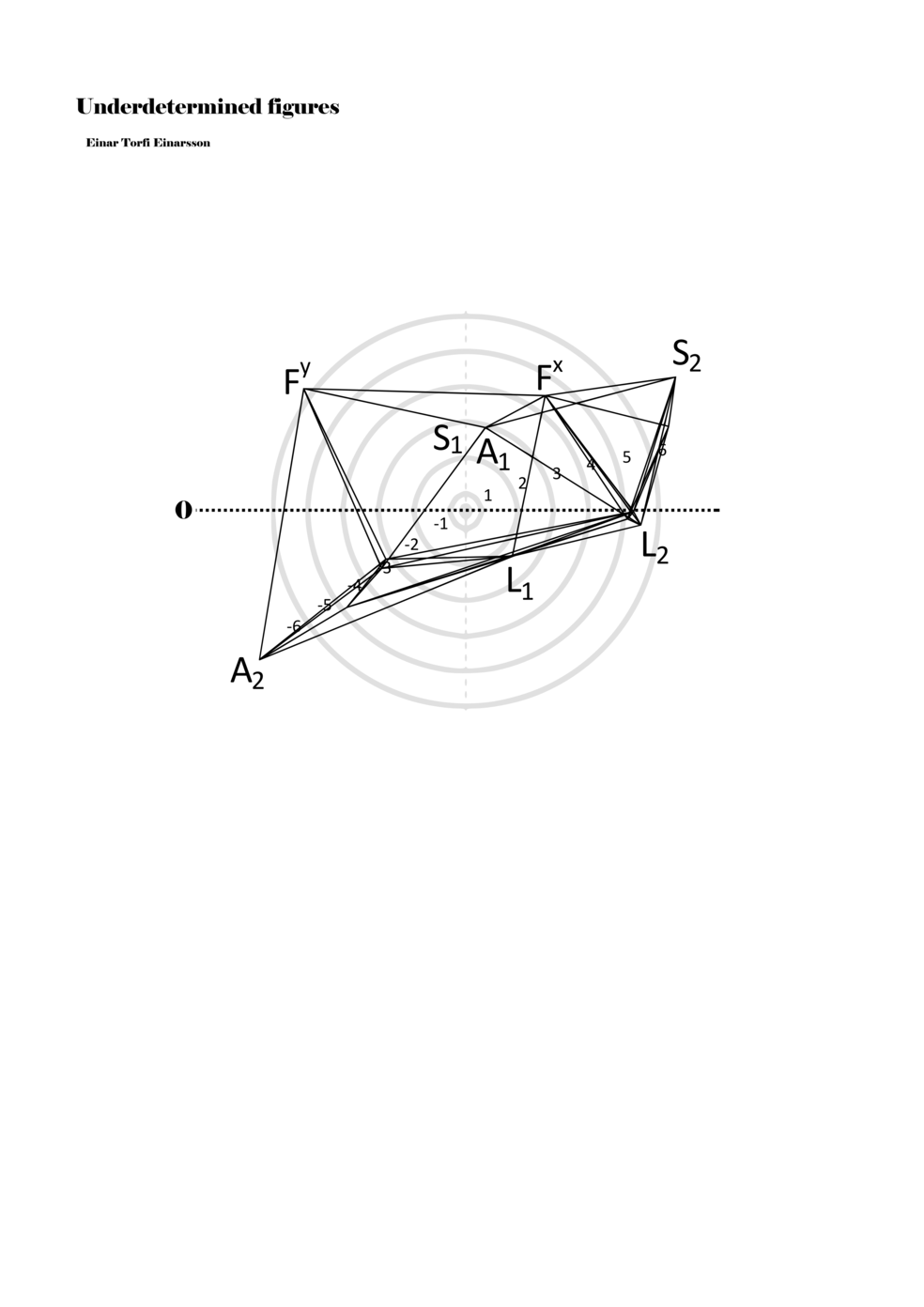
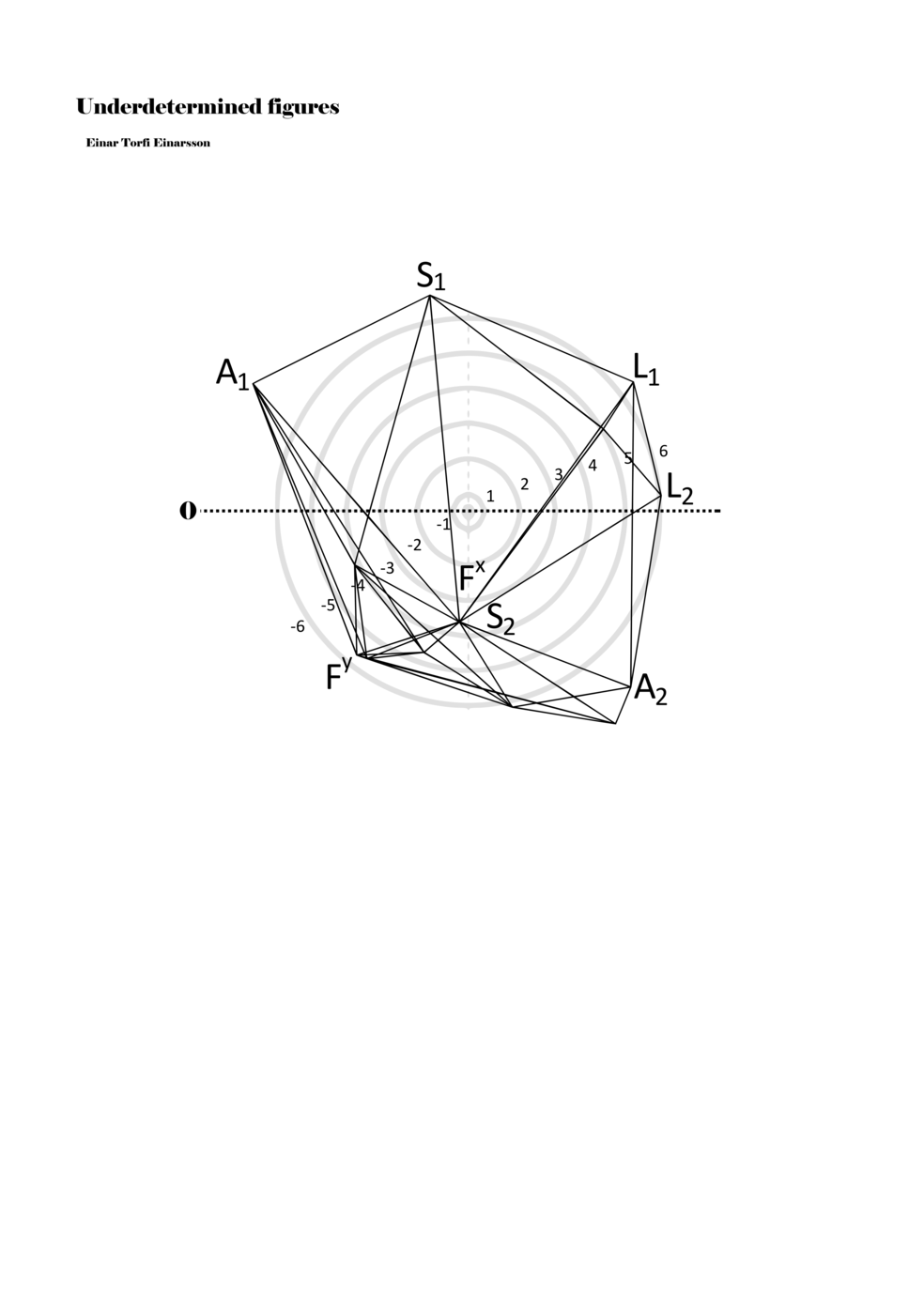
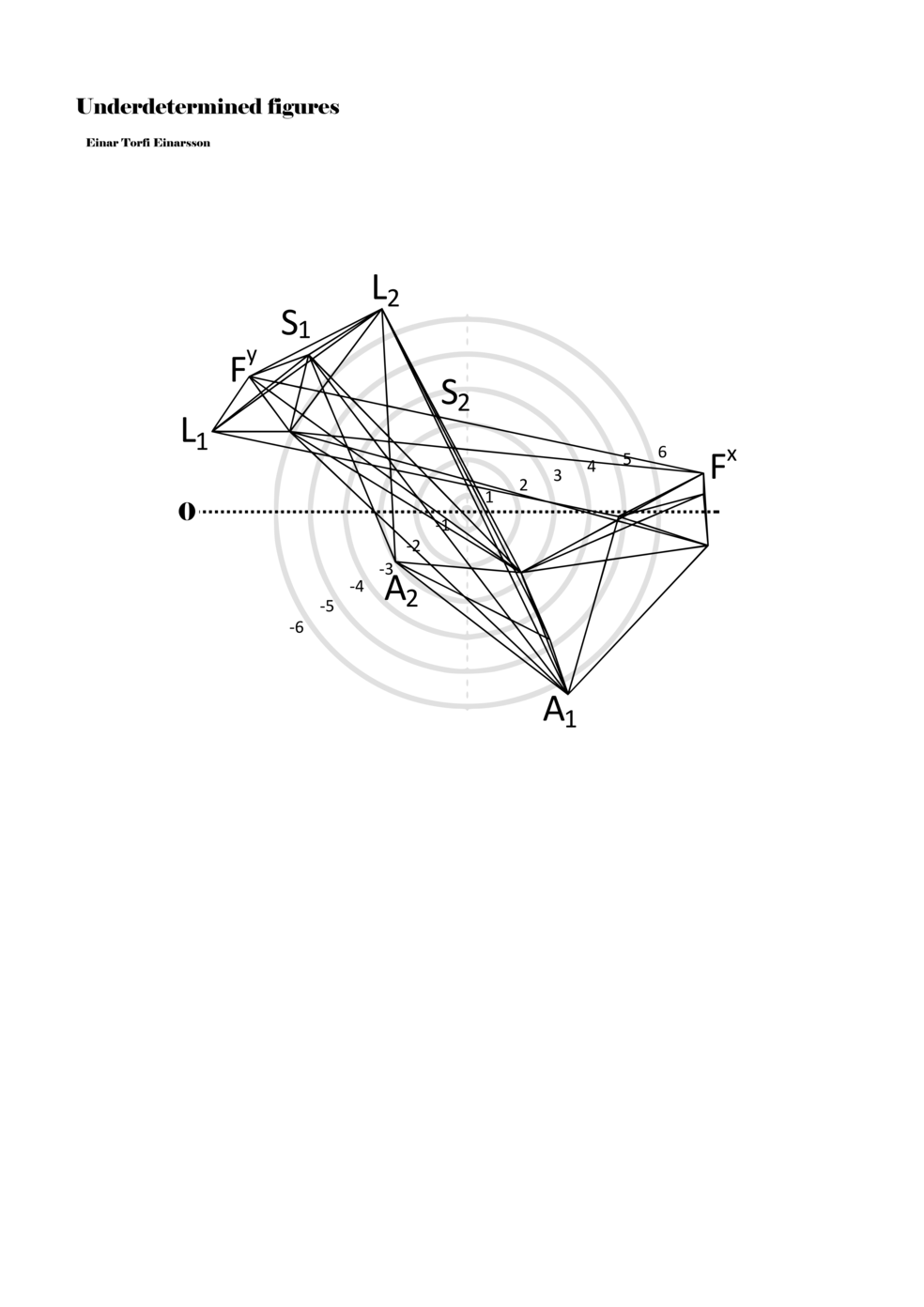
When a figure is placed within this parametric space one can thus read all kinds of changes in value when following the lines in any direction (paths). These number rows are then assigned specific physical parameters, which then operate as instructions for performers. In example 2 we see one figure placed within the field. Indicators (F, L, A, S, see details below) denote starting points (or the initial ‘posture’ of the performer) – that is, where a given parameter initiates when performing the figure. A path is chosen by the performer for each indicator/parameter but from each indicator there are several possible paths and only one path is chosen. The rule is, follow a line from the indicator to the next point (where lines join) in the figure. So, for each parameter there is a line from the indicator to the next point (or node) resulting in a change in value for that parameter. Importantly, when performing the figure all parameters are active, so the performer aims to perform all the chosen paths simultaneously. In example 2, F^x (force) initiates around -3.3 and can proceed through several paths to another point: -2, -1, +2, or -2.8, and so on. The same goes for the other indicators. Each figure is therefore a set of paths indicating a change in certain parameters, and all these paths are played simultaneously for the duration of the figure (each figure is always performed for around 2–3 seconds).

Example 2. A figure placed within the field

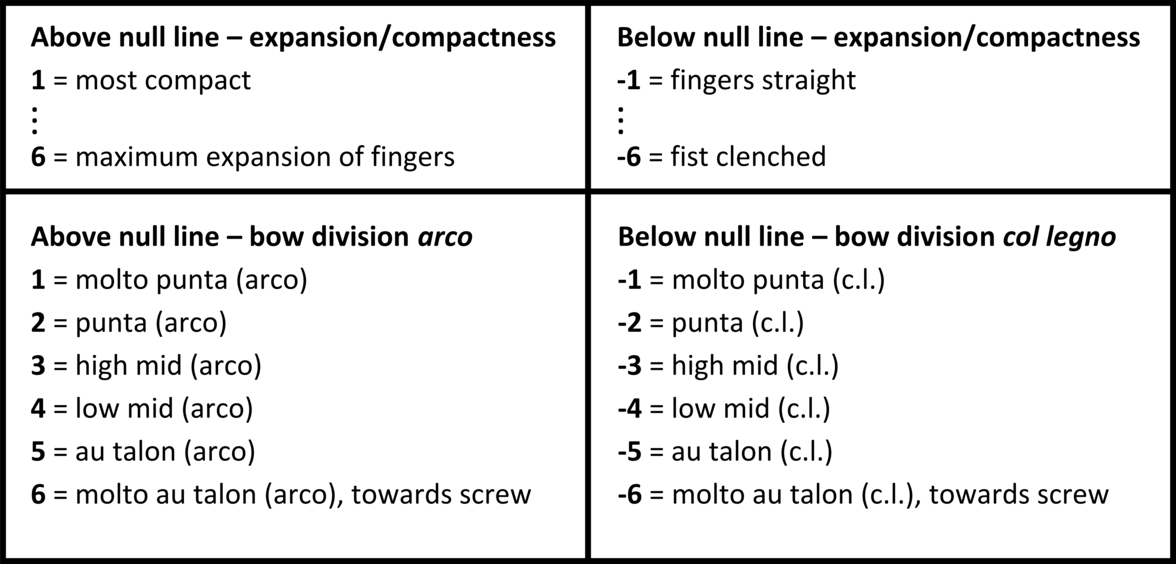
Parameters for the strings

The indicators (F, L, A, S) denoting parameters in example 2 are specifically for string instruments. The following is a delineation of these parameters.

F^x indicates the force or pressure of the action (not dynamics of sound but of physicality). It can be approached by the performer as ranging from inaudible to extreme/intense. The parametric change (-6 to +6) has the following spectrum (table 1):

Table 1. Parametric spectrum for F

F^y is only an alternative option to F^x. Thus, the same table is used only with another possible starting point. Its function is to allow the figure to have even larger possibilities of performative results.

L₁ indicates location on and around an instrument for either (a) left hand or (b) right hand (bow). The parametric change (-6 to +6) for L has the following spectrum (table 2):

Table 2. Parametric spectrum for L

For string instruments, it is necessary to indicate the location of both hands; thus L₂ is simply the location of the other hand – that is, if L₁ indicates the left hand, L₂ automatically becomes the right hand (bow), and vice versa. The performer can always choose which indicator (1 or 2) denotes the left or right hand. Therefore, both these parameters use the same table.

A₁indicates the number of fingers active on the left hand. This parameter is dependent on L; that is, when the left hand is located above the null line, and thus is within the ‘normal’ zone (see table 2), each active finger touches a separate string. When L for left hand is not located above the null line, it is possible either that this parameter can cancel itself out or that it may still be able to function as a touch element; for example, when the left hand is located somewhere on the body of the instrument, the hand can touch (or bend away from) the body with the number of active fingers indicated by this parameter. The parametric change (-6 to +6) for A has the following spectrum (table 3):

Table 3. Parametric spectrum for A

A₂ is simply an alternative option to A₁. Thus, the indications are the same but there is a different starting point.

The last parameter is S, which indicates the spread or expansion/compactness of fingers, or it can indicate bow division – that is, which part of the bow is employed (au talon/punta). The parametric change (-6 to +6) for S has the following spectrum (table 4):

Table 4. Parametric spectrum for S (upper table: spread level of fingers, lower table: bow division)

Again, if S₁ is chosen to indicate the expansion/compactness of the left-hand fingers then S₂automatically becomes an indicator for bow division.

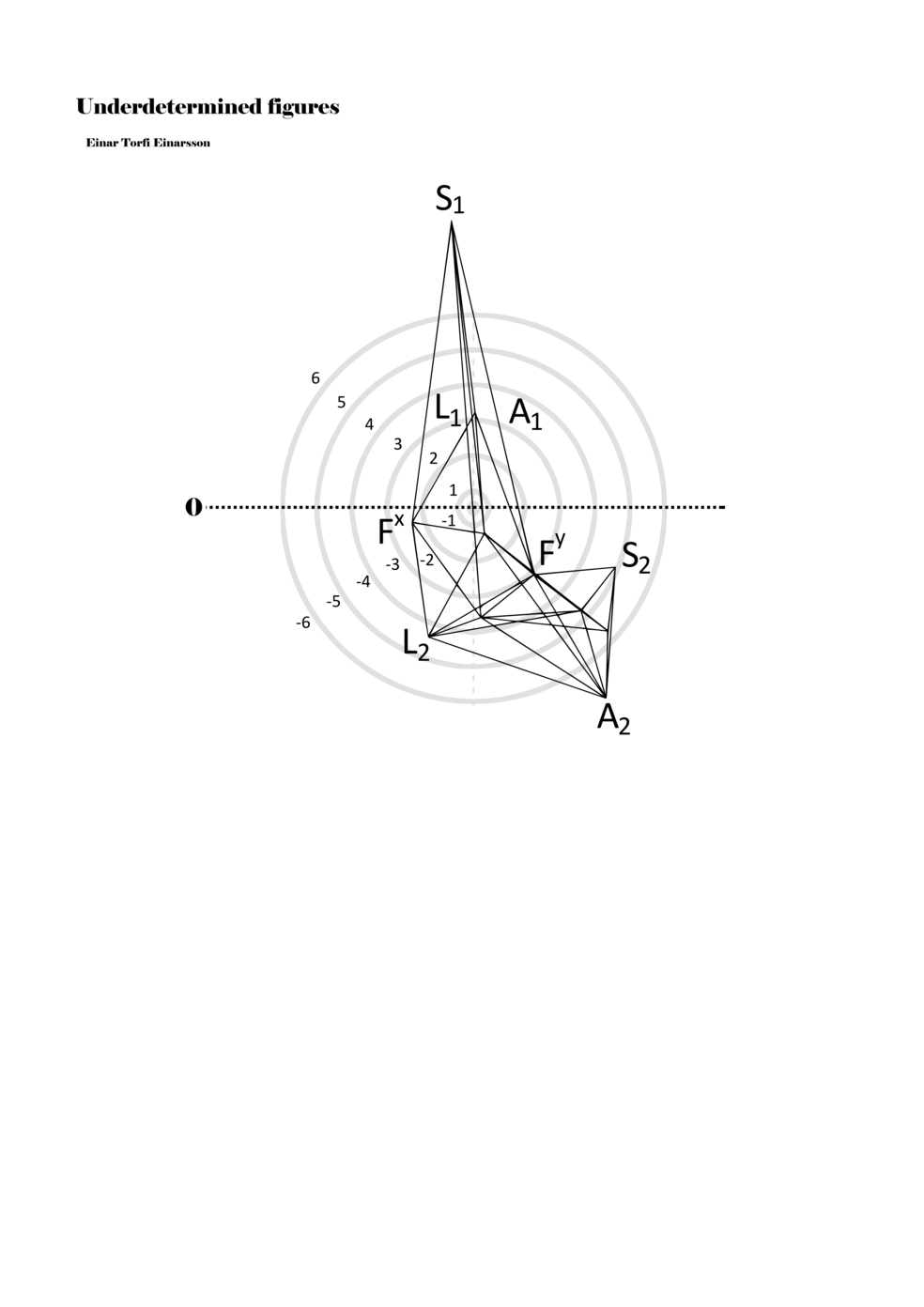
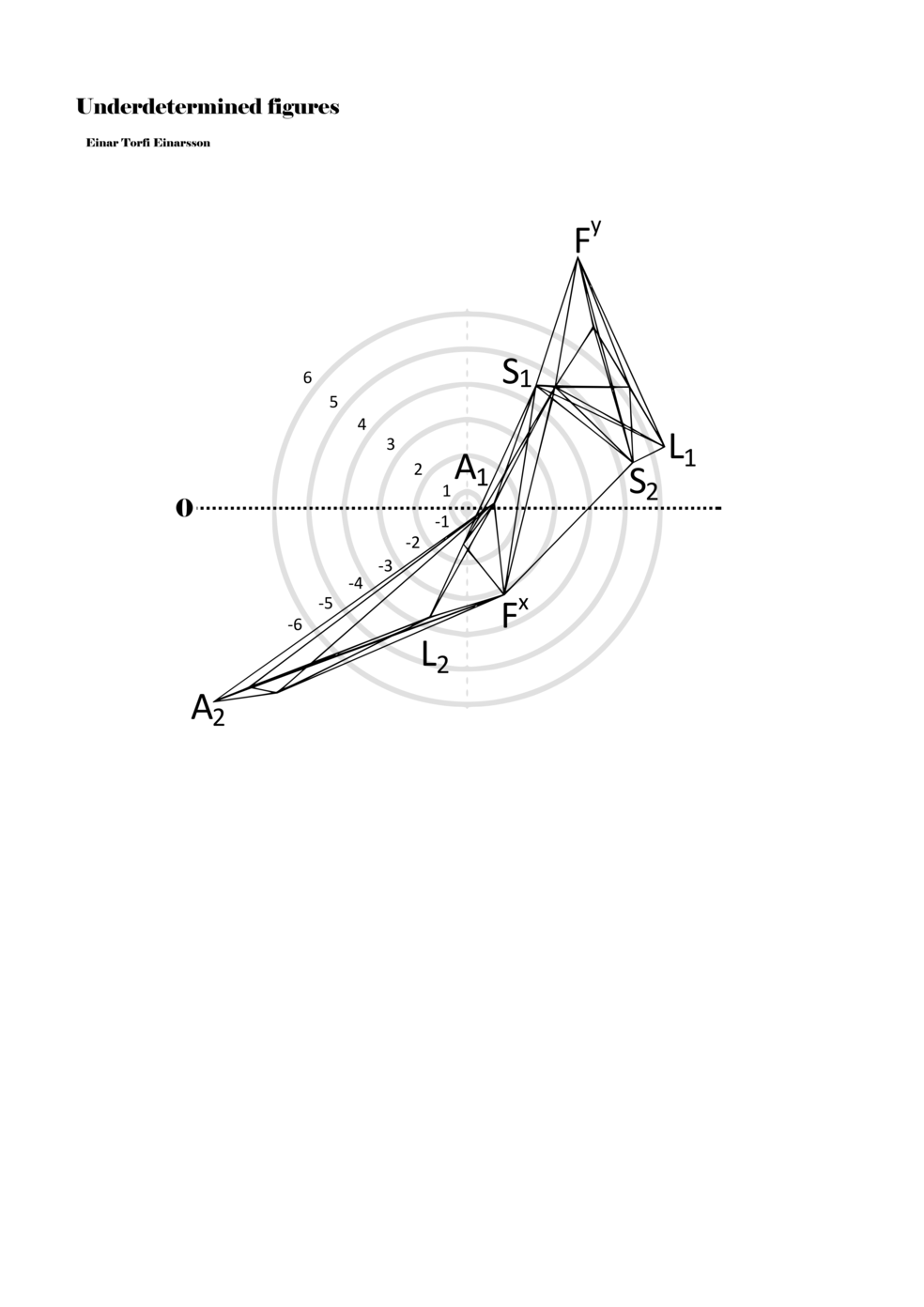
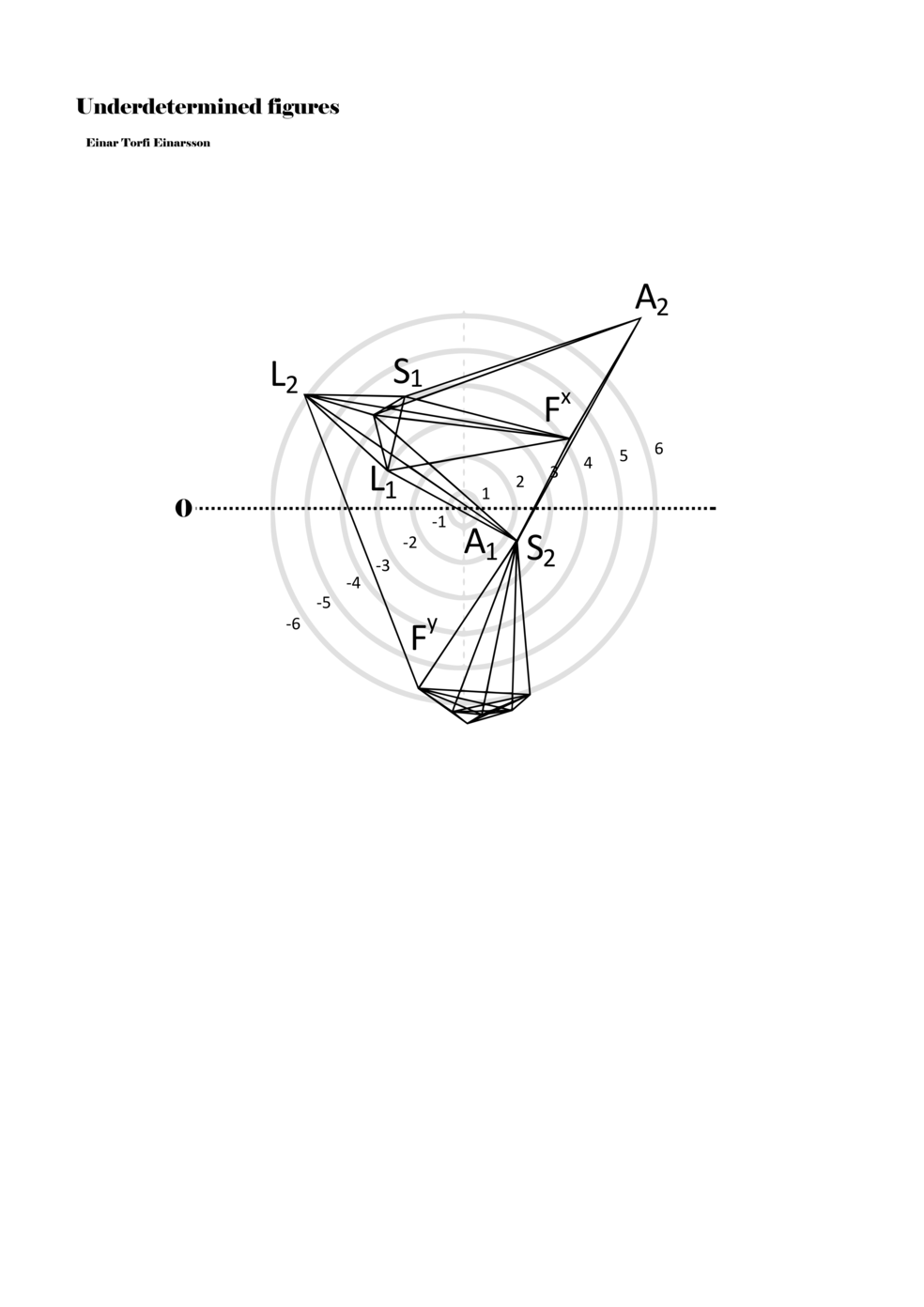
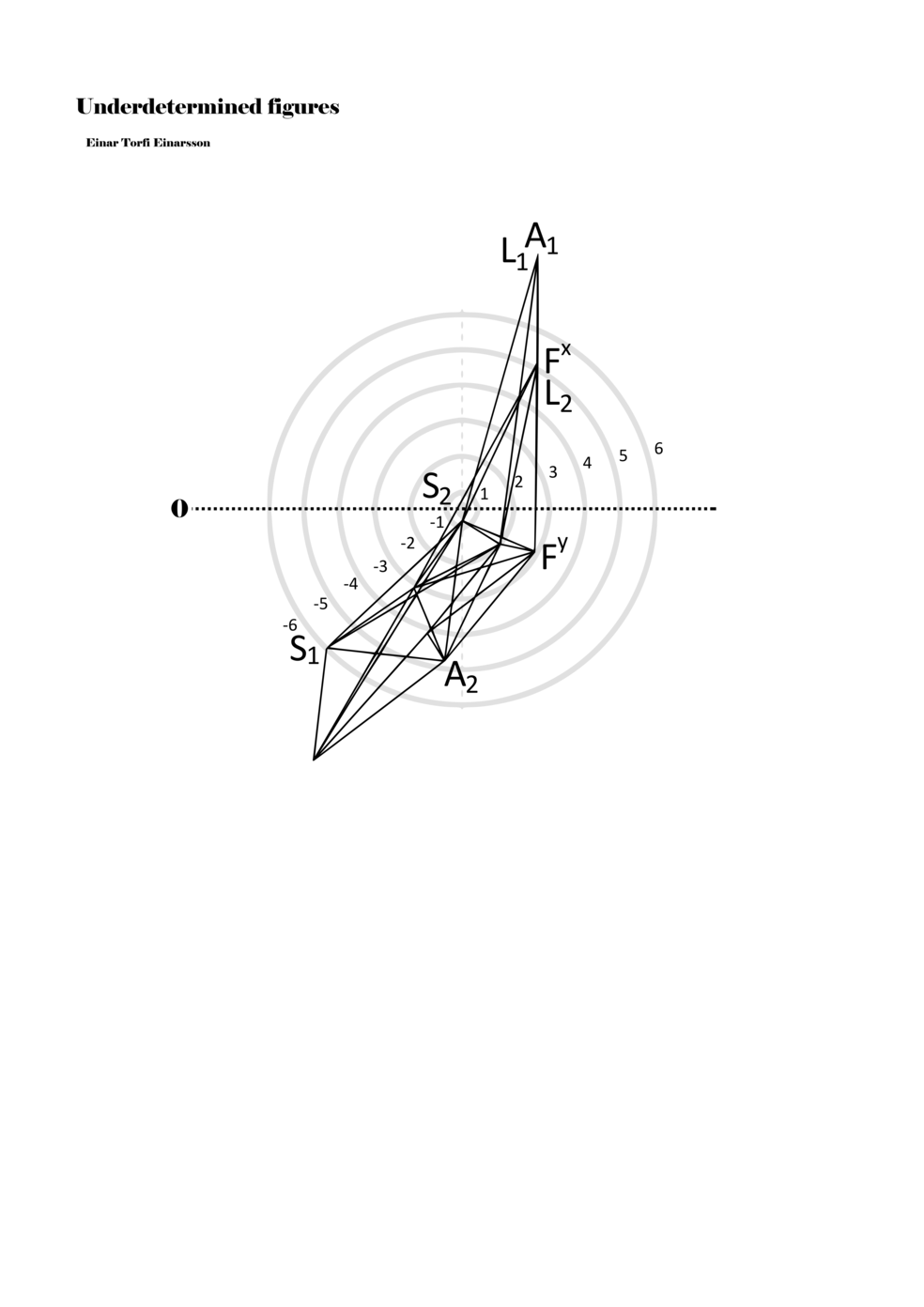
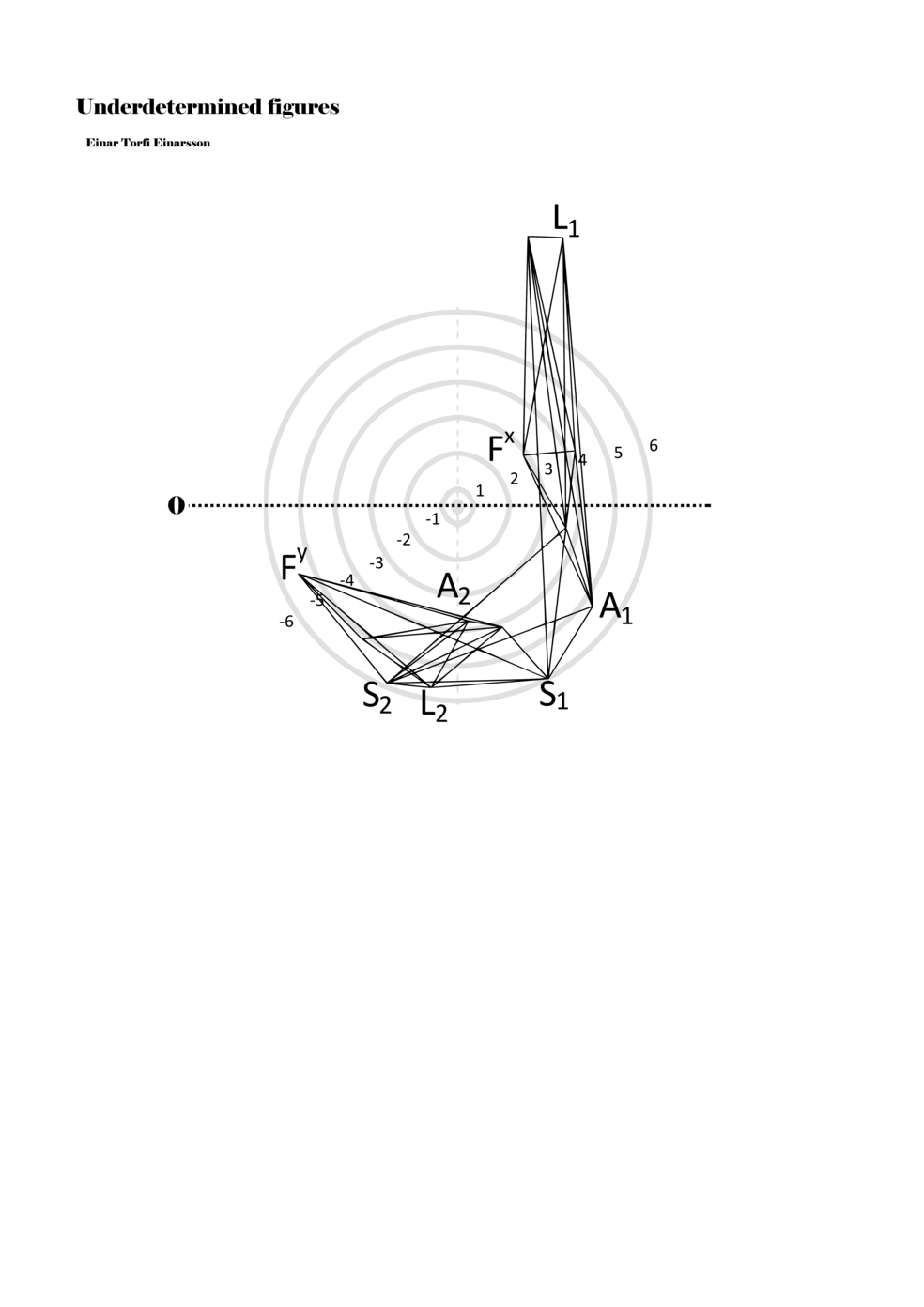
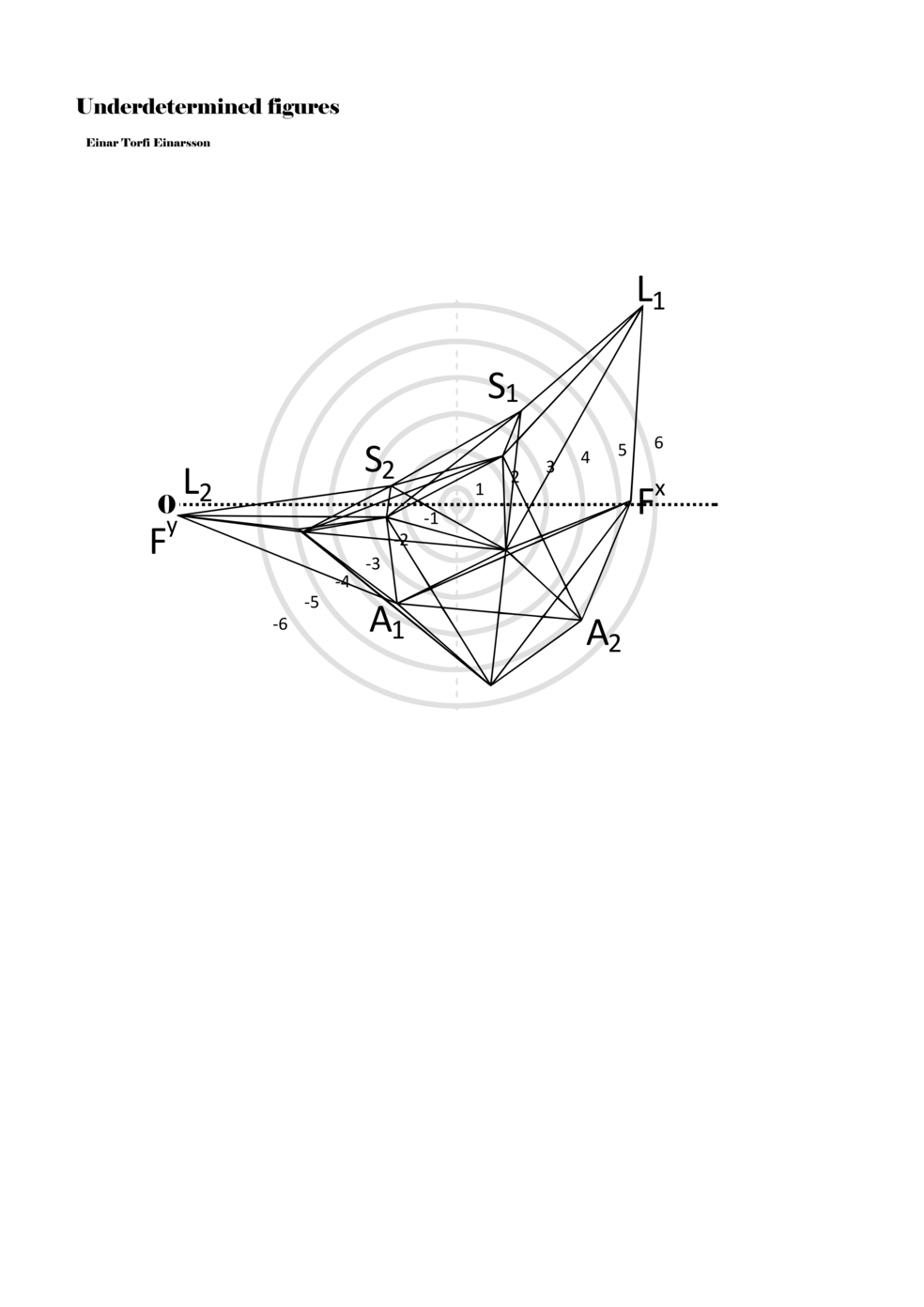
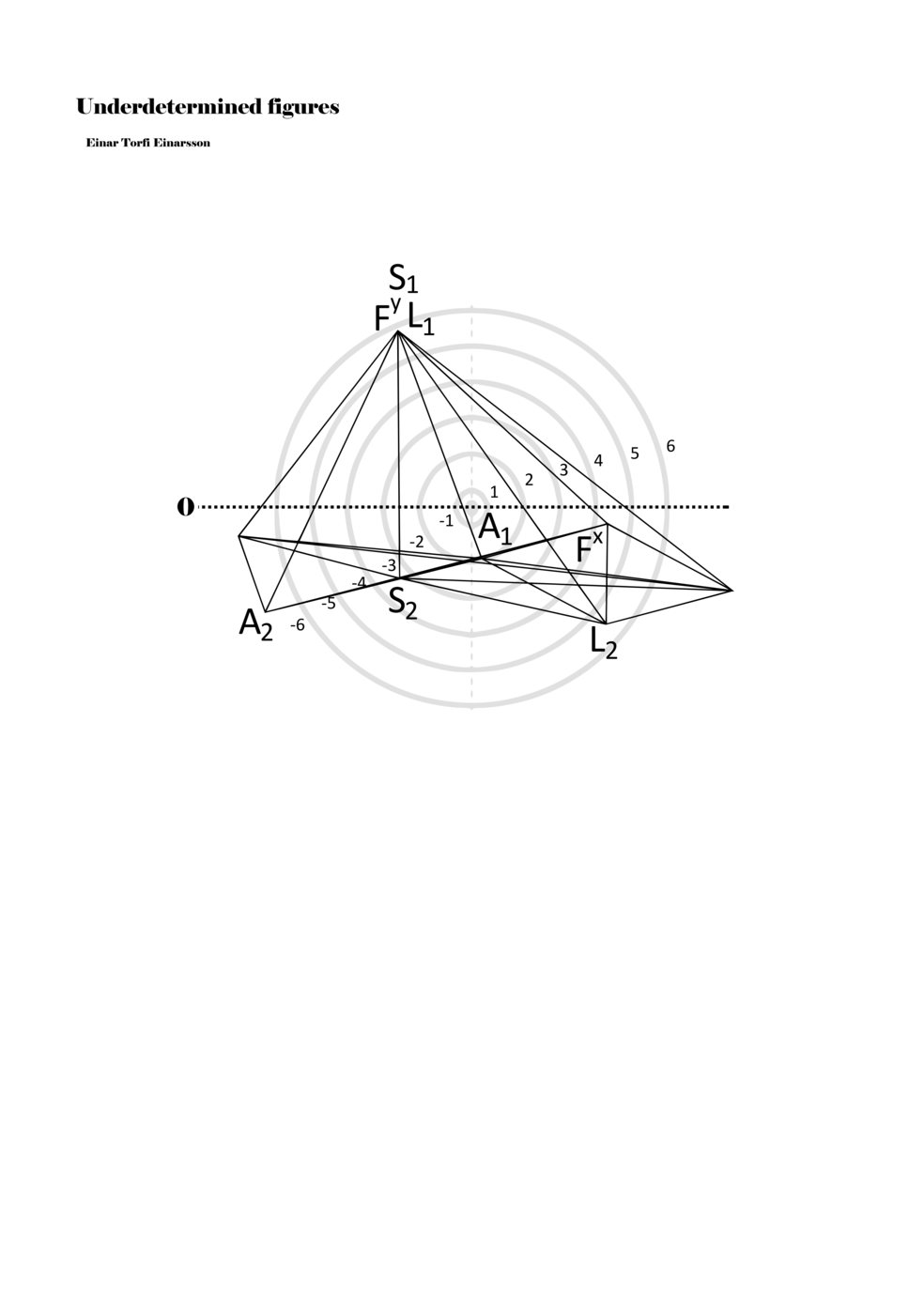
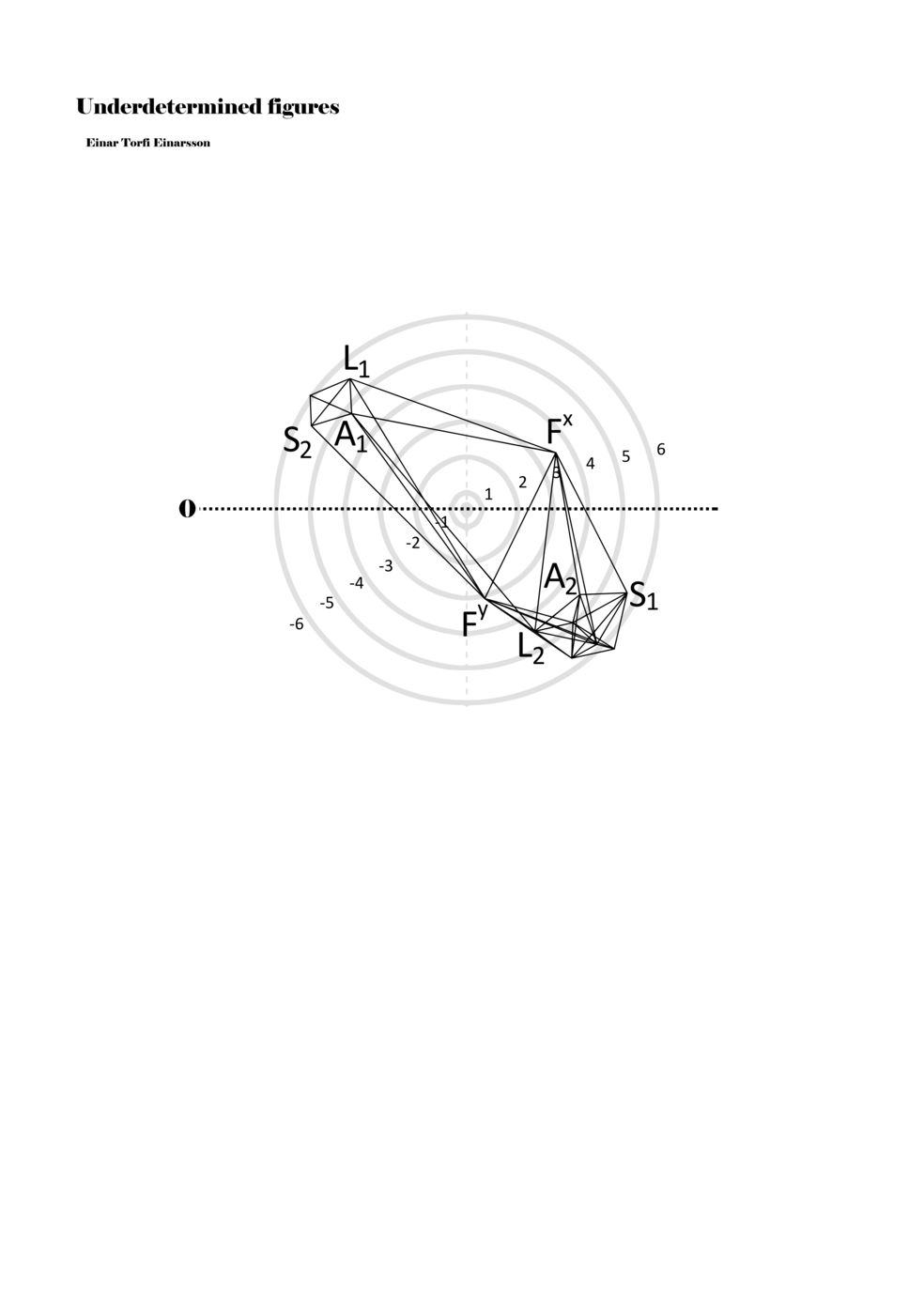
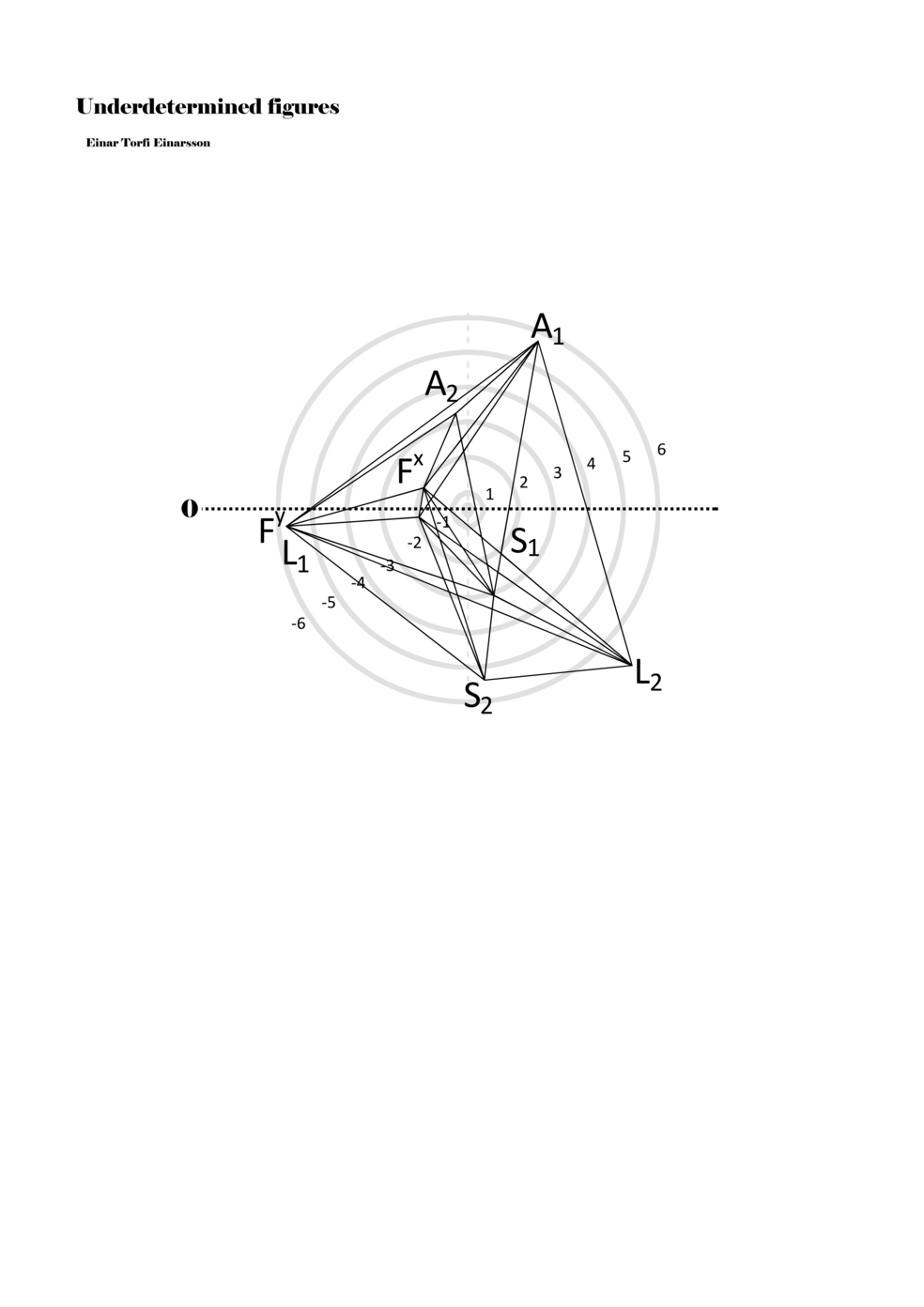
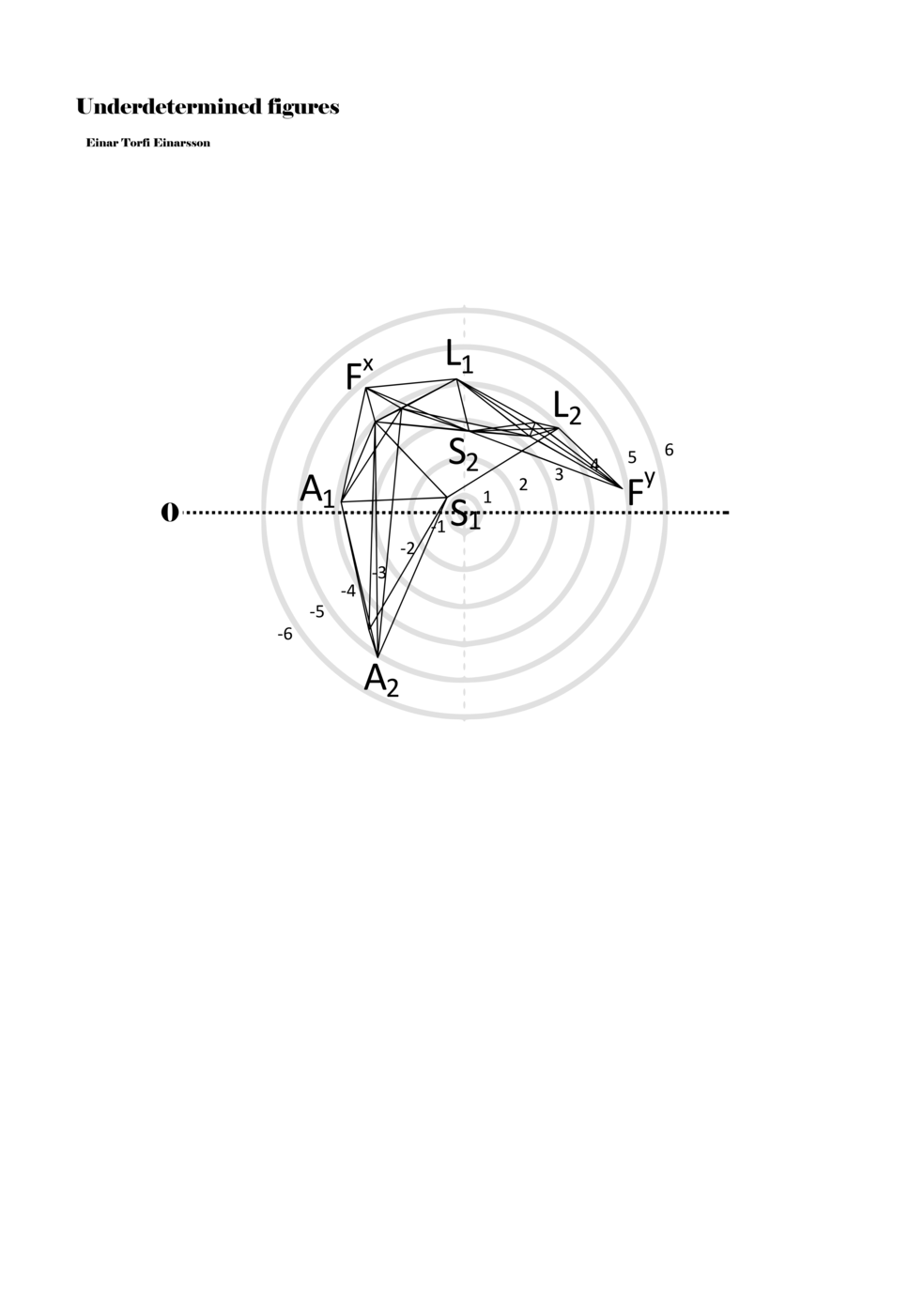
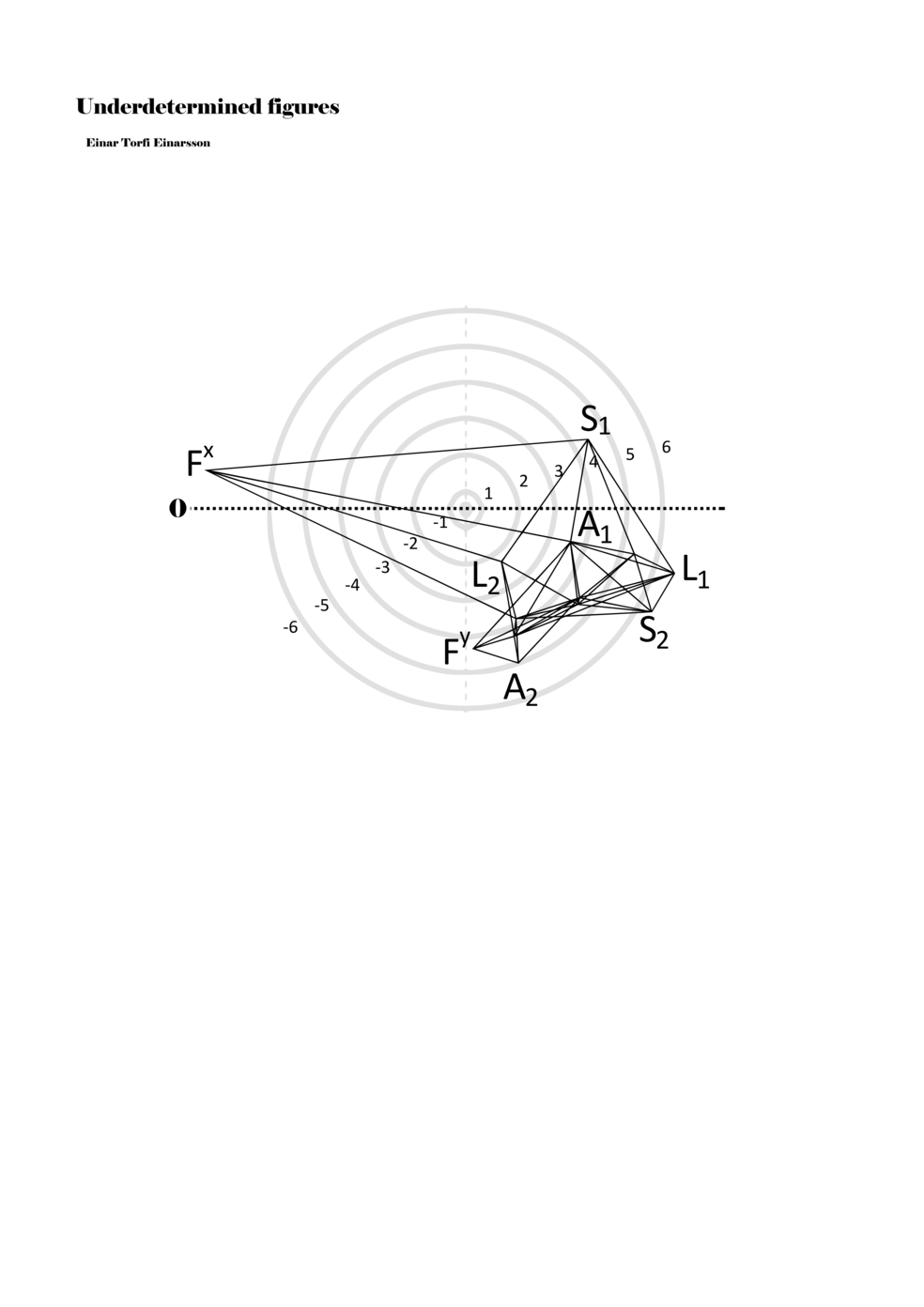
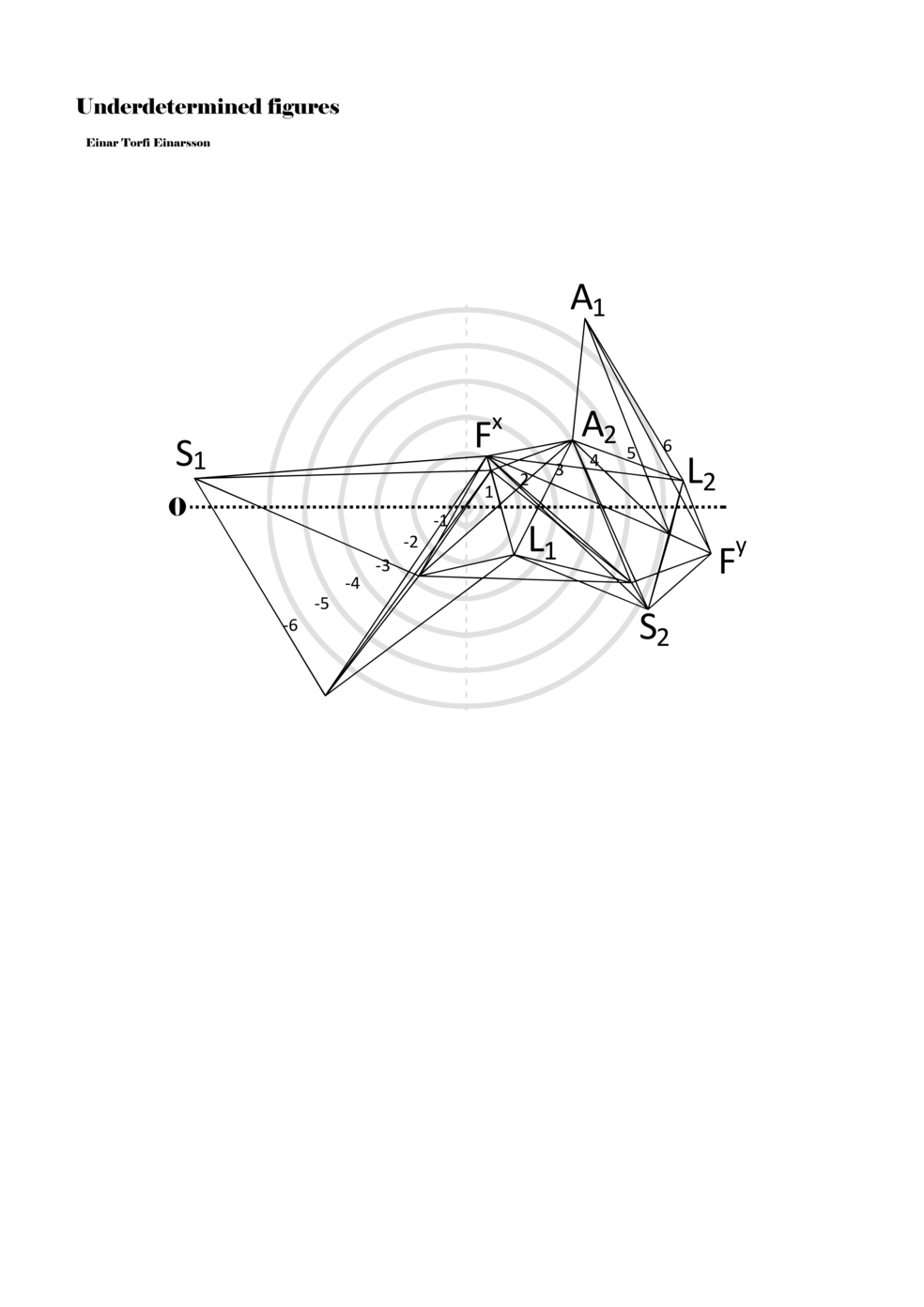
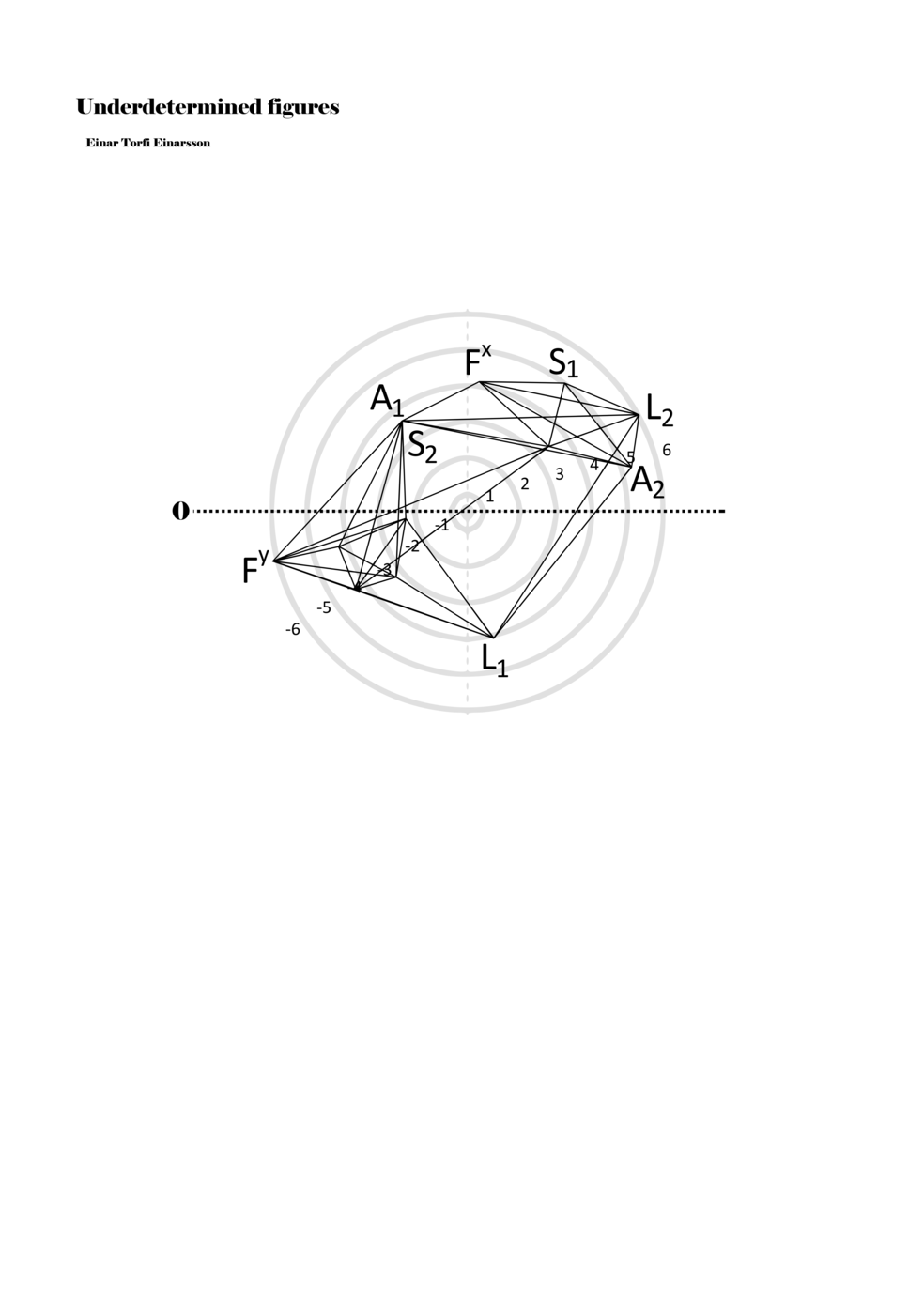
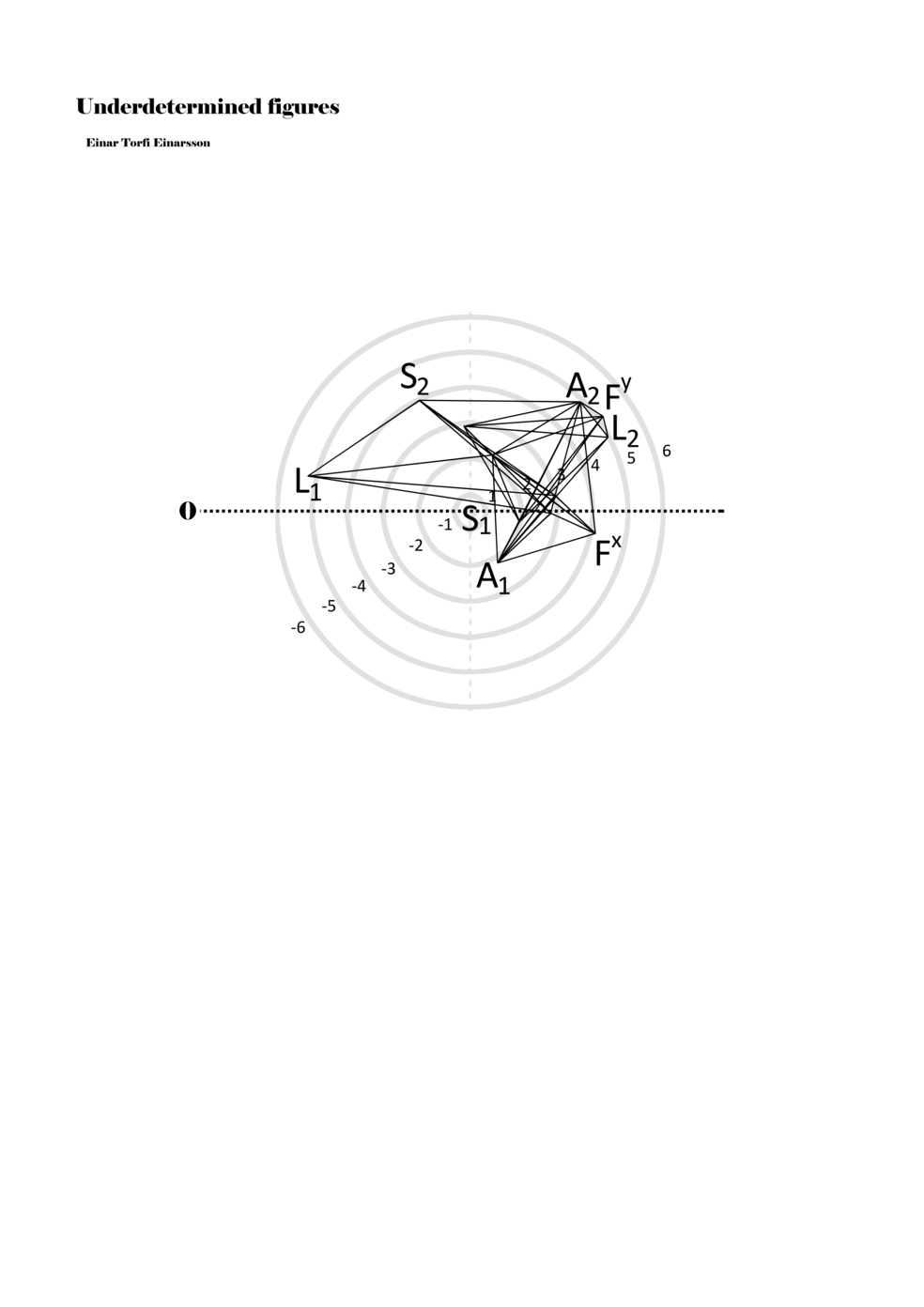
In example 3 we see a possible activation of the figure in example 2. There we see how a performer might possibly perform the figure – that is, how a performer might have to make a personal score based on my score. This concurs with the concept of proto-scores, namely that many steps might be necessary on the path to actualisation. For proto-scores to keep their virtuality (as a field of all possible connections/inclusions) they must not become scores similar to example 3, which is one step too far into actuality or fixity and therefore less of a multiplicity.

Another important aspect becomes apparent through example 3: since lines or paths are of varying lengths, the time frame for each figure (about two seconds) functions to give different speeds to each parameter. Short or long paths all have the same duration; thus, they must be performed with different speeds. In this way, each figure, when actualised, becomes a set of speed relations, and importantly ‘nothing develops, but things arrive late or early, and form this or that assemblage depending on their compositions of speed’ (Deleuze and Guattari 2004, 294).

Example 3. One possible reading of the figure in example 2

Interplay of forces

What is important to note regarding all these parameters and how they interact – and are intended to interact – both virtually in the score and actually in performance, is the possibility of their impossibility and the complexity of possible outcome and interpretation; that the piece is a multiplicity composition and therefore never in the singular. This is the intensified version of the concept of proto-object (which must remain multifarious in its many manifestations) as it translates itself, experimentally, into the notational/musical context. The moving parameters, which are a result of the specific (dis)placement of the figures within a parametric space, must be regarded as forces that can clash or even cancel one another out. In that regard, they are fundamentally open for the accidental, unpredictable, and experimental. Conclusively, proto-scores – in particular this work – are actually ‘summoning forces. […] making the invisible forces visible in themselves, drawing up figures with a geometrical appearance but that are no more than forces – the forces of gravity, heaviness, rotations, the vortex, explosion, expansion, germination and time’ (Deleuze and Guattari 1994, 182). 

References

Deleuze, Gilles, and Félix Guattari. 1994. What is Philosophy? Translated by Hugh Tomlinson and Graham Burchell. London: Verso.

———. 2004. A Thousand Plateaus: Capitalism and Schizophrenia. Translated by Brian Massumi. London: Continuum.