On Triangulation.
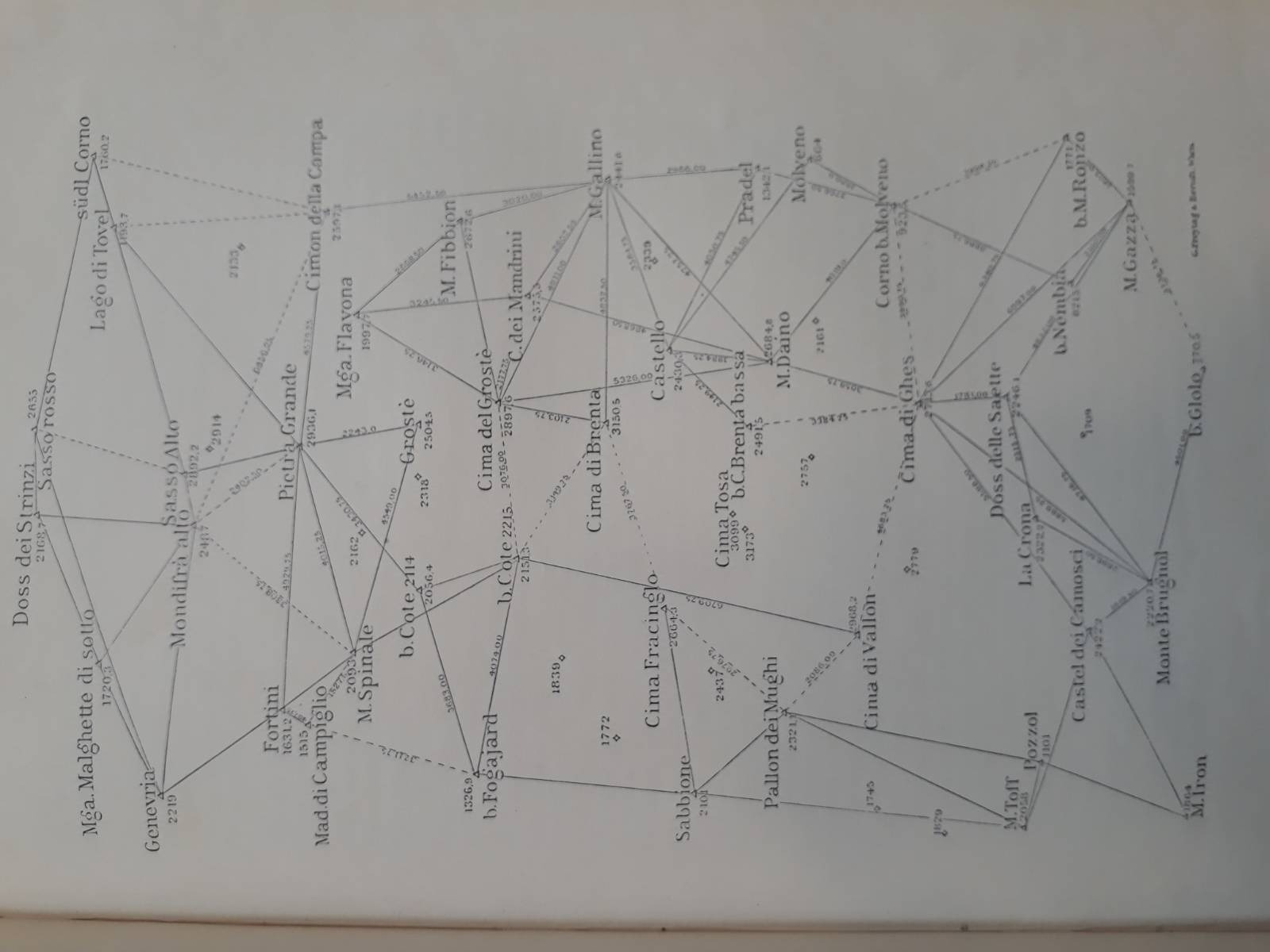
Some photos taken from the book:
L.Aegerter: "Begleitworte zur Karte der Bretagruppe", Zeitschrift des deutschen und österreichischen Alpenvereins, 19O8
Relativity theory was for physics a turning point as to how space and time and their relationship can be understood. Relativity understands space as a sort of "elastic" medium, capable of stretching and compressing: in every place, space is different. But, the major difference from the previously dominating Newtonian understanding is that time cannot be seen any more as something "absolute", i.e. an axis somehow "outside" of the world, unaffected and relentless. Time flows differently at each point. Two clocks, one on your table and one on the floor will not tick in synchrony: they don't share the same time. Each point has its own time.
There's no simultaneity hence. Except at exactly at the same place.
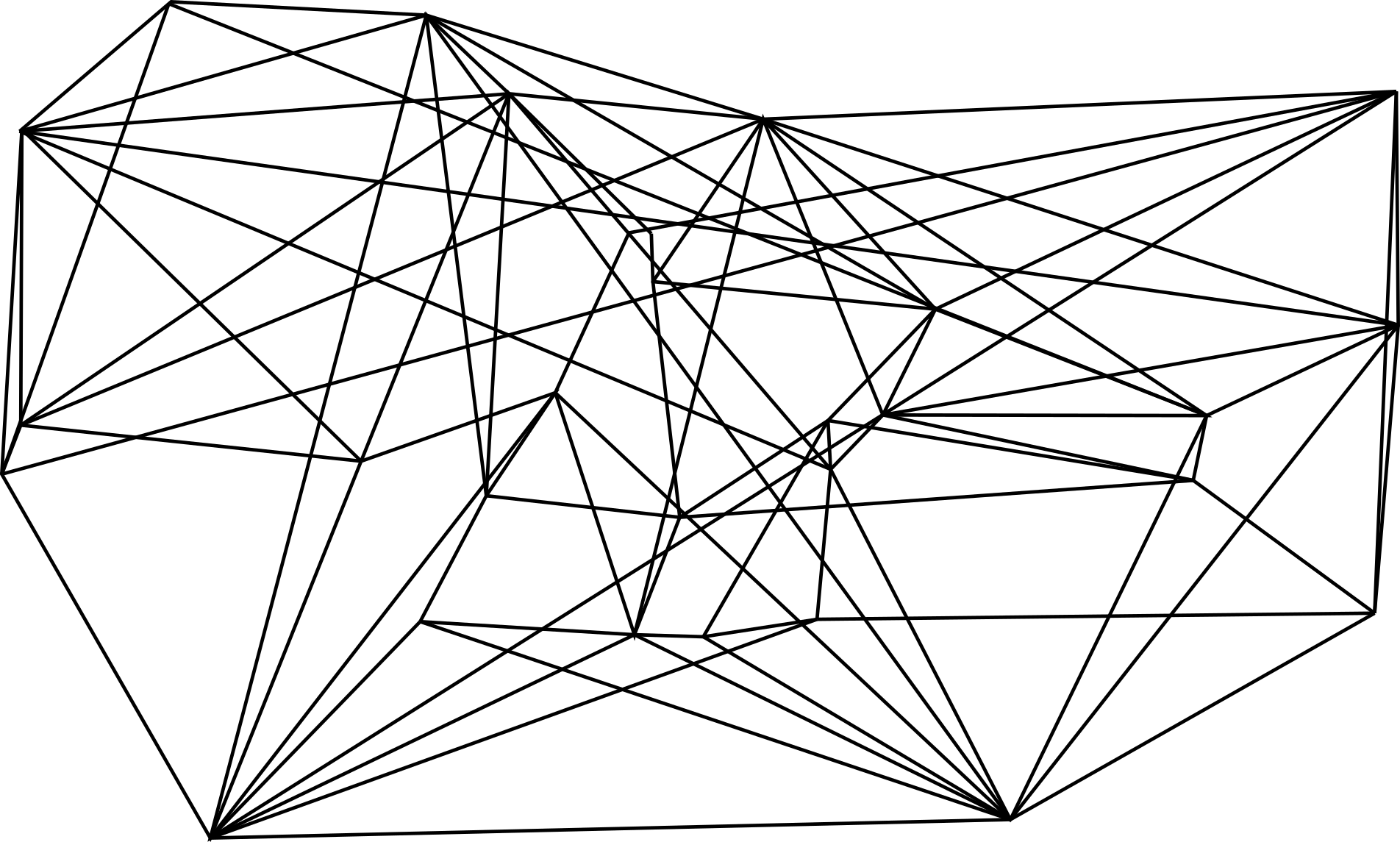
The videos in the row below refer to the second scenario: All agents seek to be at different, randomly chosen position to each other agent.
In this case, the starting conditions for the agents is "regular": they are distributed on a circle.
In each video different randomly chosen distances are used.
Eventually, configurations arrive at some stable figure, but in this case some movement (rotational) always remains. In the last video, where I used stronger pushing and pulling forces, some sort of small vibration can be seen.
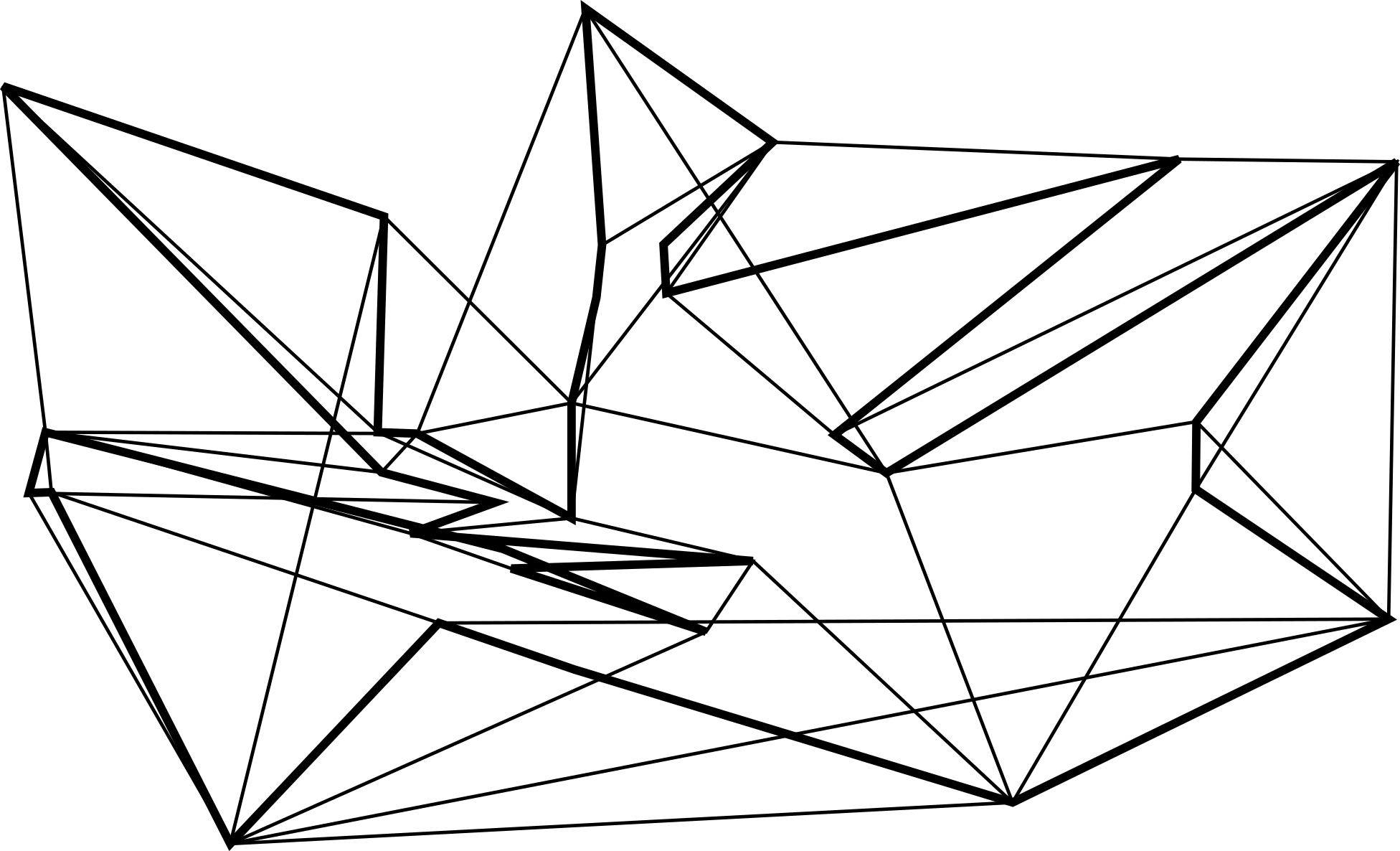
Eight points searching for space.
Somehow the idea we at came up at a certain moment in one or online meetings, that space as generated by distances stayed with me. Rather than a given "substrate", existing prior any entities in it, I resonate with an understanding of space as a "product" of differences between things.
These drawings are the product of a small series of "experiments" in which I set up a small dynamical system consisting of 8 interacting agents. Each agent "wants" to be at a certain distance to all the others: I've chosen two scenarios 1. all agents seek to be at the same distance to all the others 2. all agents want to be a different randomly chosen distances to all the others.
Agents are pushing and pulling each other, moving around trying to find the best configuration, trying to find their space. Obviously, finding a configuration which exactly satisfies the conditions in both scenarios, is geometrically impossible. Therefore, the configurations the agents generate are always approximations with respect to the scenarios "request".
The distances, the lines or forces pushing and pulling points, are not intert. Along them interacting, contact or exchange takes place.
Vibrating strings, sounding when ever a small adjustement in the space of differences take place.
Space is therefore not a given, pre-defined, texture reality.
It is made, constructed, decomposed, re-threaded. An operation, that is negotiation, among all points, agents of actors coming into contect or interacting somewhere, sometime.
How a spece is constructed, how it may evolve, is largely, if not exclusively, dependet on the attitude. How one searches, focusing on this or that.
(Re-)Constructung a space is merely an aesthetic question.
Atom", 1922 Ray Cummings)
"Space, is what stops everything from being in the same place"
("Profiles of the Future", 1962, Arthur C. Clarke)
Space is made up of differences. Space is unfolded upon distances: is
its fabric is made up of the lines connecting one point to some other
point.
To make space, means to make, define or find differences, points and
things that are not the same, that are not equal.
Space is a something that can be taken or given.
Divergence is a fundamental movement in the process of creating space.
There's still some attracting force keeping things together,
preventing them to fall into other, separate spaces: convergence.
Convergence an divergence are in a delicate, unstable equilibrium: at
any point, at any instant, a perspective may be taken that either
conflates or fragments it.
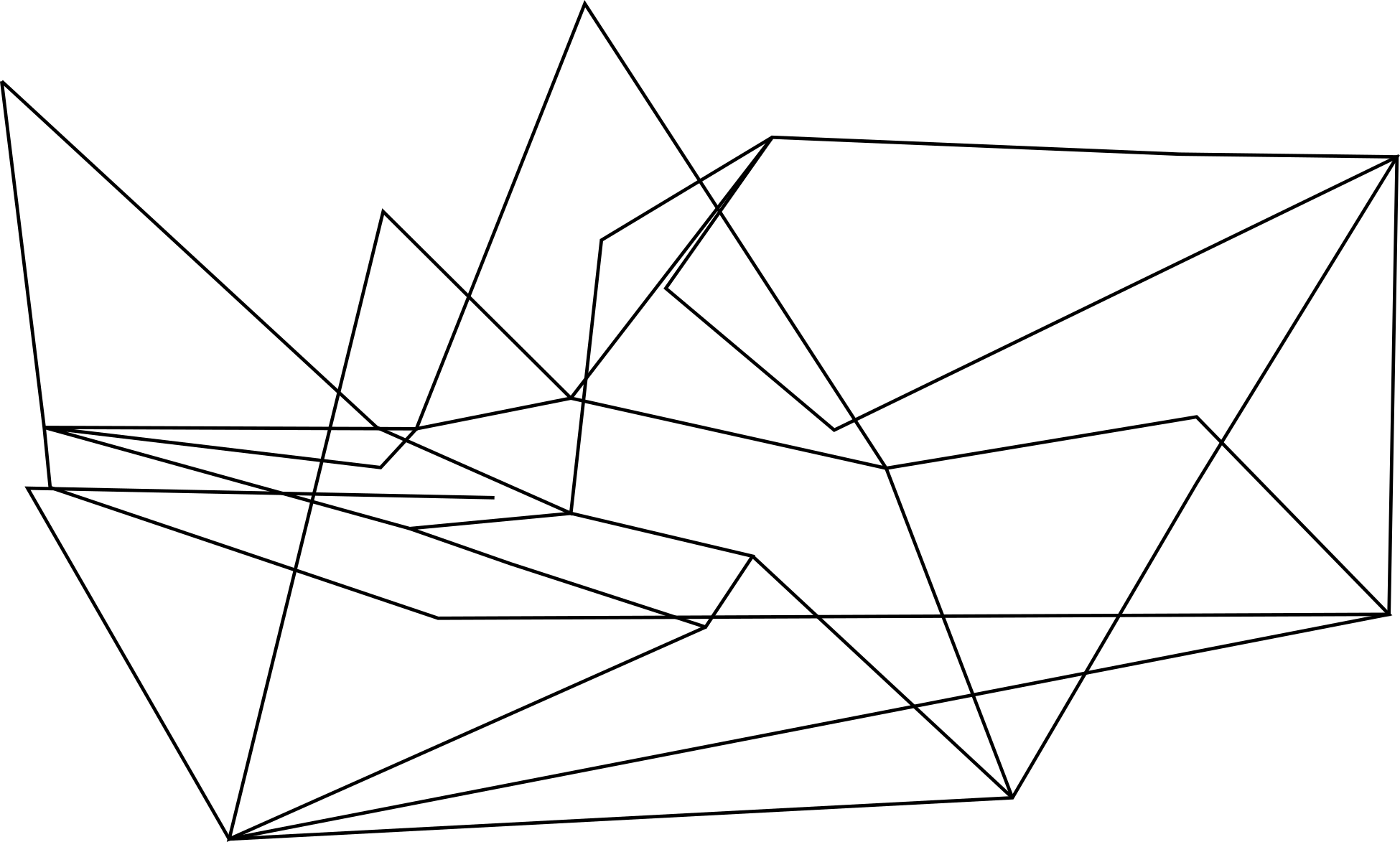
The row of videos below, depicts what happens to the agents, when taking into account that they cannot interact "synchronously", i.e. their interaction is delayed according to their current reciprocal distance. Each agent reacts according to the relativedelayed positions of all other agents. The delay is proportional to the distance: the bigger the distance between the agents, the farther in the past will be the position to which they react.
In these videos, the agents are the vertices of the lines figure: lines connect each vertex to all the others.
This first set (row) of videos are for the first scenario: All agents seek to be at the same distance to all the others.
Agents start at random distances to each other.
Configurations tend to converge or stabilize toward a somewhat regular (sometime difficult to see) figure.
I imagine joining some chosen points, with a steel piano strings (for instance 34m roll here on the left).
A network of strings.
Strings may then be put into vibration at specific points. Maybe e-bow mechanism?
Yesterday we were invited at my wife's sister for lunch. One of her kids hat this little solar powered grasshopper. It's a very tiny solar panel simply attached to a small vibration motor, similar to those built in smartphones.
I thought to couple the string vibrations to the incoming sun rays, placing one or more few of these tiny solar powered vibrators along one string. They would be then activated if an when sun would illuminate then, the speed of the rotating being dependent on how much light they would collect.
Today I bought a few of very small solar panels and motors.
henri code
# helper functions: should probably go into some general library
# all functions expect vectors
defconstant meanpos;
meanpos(x) = sum(x)/(dim(x)[0]);
defconstant magnitude;
magnitude(x) = sqrt(sum(x^2));
defconstant dist;
dist(x,y) = magnitude(x - y);
defconstant norm;
norm(x) = x/(magnitude(x) + 0.0000001);
scopelen = 2000;
scopesec = 1.0 / scopelen;
# begin: define system of 8 3-dimensional agents
# each will interact with all other agents in the system
def agent{48000}[8,3];
# array of distance factors
def distances[8,7];
# initialise distances randomly ar regularly between 1.0 and 5.0
distances = 4.0;
# distances = 3.0 + 2.0*noise();
def mag;
mag = 1.0;
[agent[i, 0] = 2.0 * sin(i/8.0*pi2), agent[i, 1] = 2.0 * cos(i/8.0*pi2)]; # regular initial condition
# agent = noise() * 4.0; # random initial condition
#visualization
(scope[d]() = agent[d/2,0]) ~ (d=[0:15:2]);
(scope[d]() = agent[d/2,1]) ~ (d=[1:15:2]);
# remove baricenter translation
agent[i,j]() = agent[i,j] - meanpos(agent[[:],j]);
def rit;
rit = -20000;
def dydist[8, 8];
dydist[i, j]() = dist(agent[i,[:]], agent[j,[:]]);
def dyritdist[8, 8];
dyritdist[i, j]() = dist(agent[i,[:]], agent{dydist[i,j] * rit}[j,[:]]);
def dynorm[8,8,3];
dynorm[i,j,k]() = - ((agent[i,[:]] - agent{dydist[i,j] * rit}[j,[:]])[k] / ( dyritdist[i,j] + 0.0000001));
agent[i,j]'() = (dynorm[i,(i+1)%8,j] * (dyritdist[i,(i+1)%8] - distances[i,0])
+ dynorm[i,(i+2)%8,j] * (dyritdist[i,(i+2)%8] - distances[i,0])
+ dynorm[i,(i+3)%8,j] * (dyritdist[i,(i+3)%8] - distances[i,0])
+ dynorm[i,(i+4)%8,j] * (dyritdist[i,(i+4)%8] - distances[i,0])
+ dynorm[i,(i+5)%8,j] * (dyritdist[i,(i+5)%8] - distances[i,0])
+ dynorm[i,(i+6)%8,j] * (dyritdist[i,(i+6)%8] - distances[i,0])
+ dynorm[i,(i+7)%8,j] * (dyritdist[i,(i+7)%8] - distances[i,0])
+ dynorm[i,(i+8)%8,j] * (dyritdist[i,(i+8)%8] - distances[i,0])
)*mag
- att * _[i,j];