12+13 Aug; we're now moving towards 'text fronts', creating compound graphs from all pairs of three texts (the two long segments from Gertrude's text, and a third text assembled from five shorter segments; the lengths are 818, 806, and 775 words).
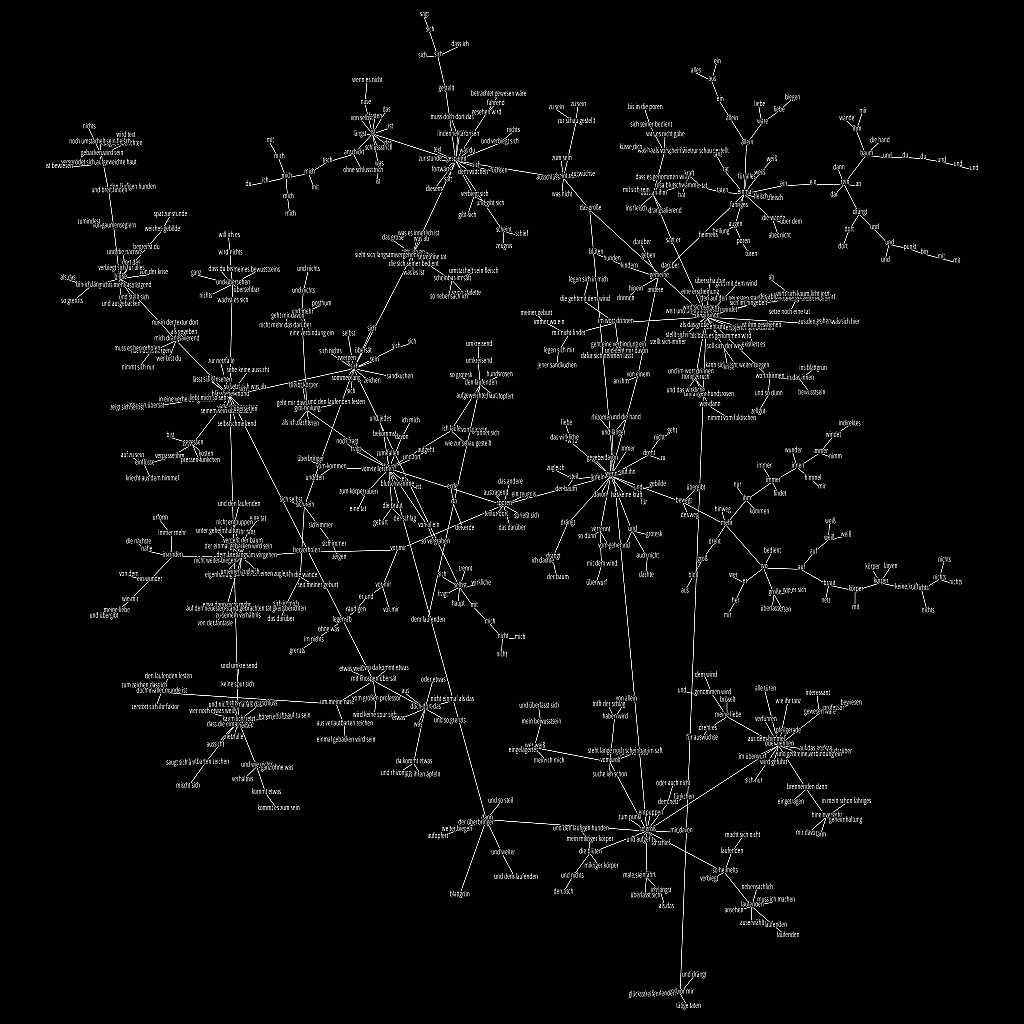
Texts 1 and 3 are shown here, forming a compound minimum spanning tree from all pairwise similarities, revealing the cross-over and also segregation between the texts (red versus green).
{kind: note, function: contextual, group: colours}
Minimum spanning trees are a form of topological learning, such that short, non-recursive paths are built across a graph (network) of objects, taking into account their proximity or edge weights. Here the edge weights were the visual correlation (typographical similarity) between pairwise words of the first section of Gertrude’s text.
{function: contextual, group: mst}
The relaying of sound across the speaker network could follow MST as well. A word is ejected at one node and travels through a hidden tree to another node where its transformation is injected. I calculated the pairwise similarities based on the short-time MFCC of the spoken recording, beginning with the first section of the text, "Da dreht sich der Baum…". The first image was a surprise - it looked very different from the trees constructed through typographical similarity.
{kind: caption, group: mst2}
vertex "3- 6: noch"
vertex "3- 36: noch"
vertex "1-700: nicht"
vertex "3-497: nicht"
vertex "1-504: mich"
vertex "1-477: mit"
vertex "1-777: selbst"
vertex "1-508: sandkuchen"
vertex "1-137: sich rein"
vertex "1-595: sagt er"
vertex "1-479: sich nur"
vertex "1- 57: und mehr"
vertex "1-579: gibt heilung"
vertex "3-257: behandeln"
vertex "3-349: den anderen"
vertex "1-311: oder dehnen"
vertex "3-461: von dem"
vertex "3-139: vermählt"
vertex "3-187: einmal"
vertex "1-490: einmal"
vertex "3- 55: reine"
vertex "3-425: rein"
vertex "1- 16: ein"
vertex "1-774: ein"
vertex "1-138: rein"
vertex "3-163: kann"
vertex "1- 17: und"
vertex "1- 22: und"
vertex "1-806: punkt"
vertex "1-262: und"
vertex "1-242: bin"
vertex "1-261: mit"
vertex "1- 24: mit"
vertex "1-600: du"
vertex "3-116: ich"
vertex "1- 23: ich"
vertex "3-254: nicht"
vertex "1- 15: mich"
vertex "1-105: mich"
vertex "1- 28: tisch"
vertex "3-638: im stift"
vertex "1-165: blutschwämme"
vertex "1- 4: baum"
vertex "1- 26: erde"
vertex "1- 35: sporen"
vertex "1-129: gespannt"
vertex "1- 85: sich larven"
vertex "1-817: sich"
vertex "3- 92: nach harz"
vertex "1-166: mit knospen übersät"
{kind: code}
How do we generate paths through the speaker network with the path lengths as a given constraint? Picking random start (ejected) and end (injected) word will not yield a path of size 30 or higher, and in average be much smaller.
Through experimentation, the following algorithm was devised:
- we generate an initial path from the ejected and injected words using the DFS in the "main" MST
- repeat while the currently generated path length is smaller than the desired path length:
- pick a random edge along the current path
- "cut the path" by removing the edge from the set of all edges
- recreate an MST from all vertices minus the vertices already on
the path, with the exception of the two thus determined boundary
vertices
- find the path in the new MST for the two vertices, using again DFS
- splice this new path into the path of the previous iteration at the
cutting point
- finally, if the resulting path becomes longer than the desired path, drop random elements along the last iteration of the path.
The left hand side shows a path of target length 50 thus generated.
{function: description, keywords: [ algorithm, mst, paths, spatialization, speakers]}
// depth-first-search
source = "783: nur in der textur dort", sink = "111: aus"
Path:
"783: nur in der textur dort"
"449: mich drangsalierend"
"346: blässlicher mond"
"817: sich"
" 85: sich larven"
"129: gespannt"
"670: scheint mir"
" 50: das große"
" 46: so groß"
"530: dann"
" 4: baum"
" 26: erde"
" 35: sporen"
"374: wenn"
"213: bewegt"
"212: mehr"
" 9: dreht"
" 47: groß"
"766: bloß"
"111: aus"
{kind: code}
How could it be so "hierarchical", with typically very short words at the high-degree nodes? I had forgotten the inversion from similarity to MST "cost" factor. In order to keep similar nodes together, one has to assign these edges relatively small weights ("costs"). Correcting with cost = 1 - normalised_similarity, the structure looked familar again.
{kind: caption, group: mst3}
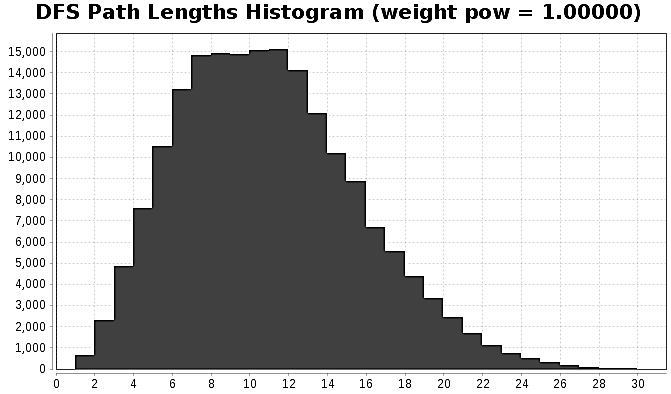
mean path length = 10.8546, median = 10, min = 1, max = 31
(lengths means number of edges to traverse)
{kind: caption, group: isto1}
First runs reveal some interesting properties of this simple algorithm (traversing the paths). The "central" words form easily distinguishable marks, such as "der großen / das große…". And some patterns also recognisable as forward / backward, e.g. "baum / erde / sporen", "sporen / erde / baum".
{kind: note}
// depth-first-search
source = "499: von der fantasie", sink = "623: ein"
Path:
"499: von der fantasie"
"432: etwa dann nicht mehr"
"583: dem brennenden dann"
"642: hervorholen"
" 36: vor mir"
" 35: sporen"
"374: wenn"
"172: von einem"
"154: gemeine"
"490: einmal"
"402: allein"
"267: allein"
"623: ein"
{kind: code}
It seems I have to correct myself - the paths statistics are identical, no matter what exponent we use in the cost function. The difference in image above must be something purely related to the force-directed graph layout.
Looking again at the Kruskal algorithm, there is indeed no notion of the cost values, instead everything simply relies on the sorted order of costs, and this order is not affected by the exponent.
{kind: note}
What would happen if the cost function is biased towards higher or lower similarities? I rendered a variant with cost = (1 - sim).pow(2.0). In other words the costs of traversal along moderate similar edges decreases. It appears that the hierarchy increases, that is there is less branching, as traveling along multiple nodes on one branches has become more acceptable.
{kind: caption, group: mst4}
// depth-first-search
source = "719: und jedes", sink = "253: seine stafette"
Path:
"719: und jedes"
"249: bekommst"
" 4: baum"
"530: dann"
" 46: so groß"
" 50: das große"
"670: scheint mir"
"129: gespannt"
" 85: sich larven"
"191: scheinbar im saft"
"253: seine stafette"
{kind: code}
---
meta: true
project: SchwaermenVernetzen
keywords: [minimum spanning tree, topological learning, proximity, algorithm, words, text]
---
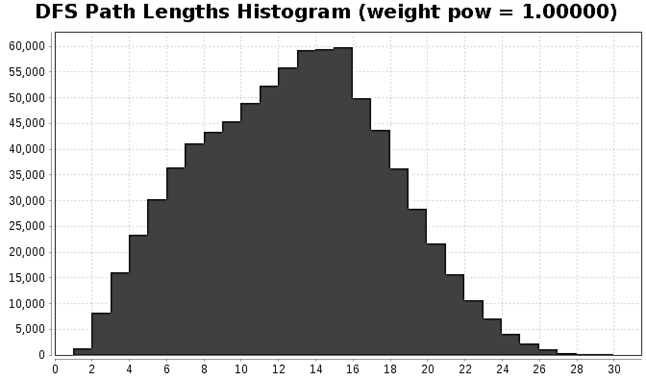
the histogram of DFS path lengths through the combined texts 1 and 3 increases the median from 10 to 13
{kind: caption, group: isto2}
// depth-first-search
source = "19: blüten", sink = "282: laufenden"
Path:
" 19: blüten"
"291: hunden"
"275: kindern"
"154: gemeine"
"172: von einem"
"374: wenn"
" 35: sporen"
" 26: erde"
" 4: baum"
"530: dann"
" 46: so groß"
"103: so heimelts"
"282: laufenden"
{kind: code}