(2019) The Singing Violin: Portamento use in Franz Schubert’s violin music

Emma WIlliams

(this research was submitted March 2019) How can late-18th- and early-19th-century vocal techniques influence our way of experimenting with portamento use in Schubert’s violin music and how can we reinstate the practice in ways that are relevant for current listeners and players? The voice and violin have always shared an intimate connection. Violin treatises from the late-18th and early-19th centuries consistently encourage violinists to imitate vocal techniques. My thesis explores this relationship via the music of Franz Schubert (1797-1828), who revolutionised Lieder and used vocal techniques in his instrumental writing. Many fundamental vocal expressive devices, including portamento, have been lost in “modern” and “historically-informed” (HIP) singing and violin playing. My thesis aims to (1) understand the historical appropriateness of portamento in Schubert’s violin music and how different types of portamento work, (2) examine why the technique was lost, and (3) explore ways of reigniting it in today's musical aesthetic. I first analysed relevant written sources and early vocal and violin recordings, finding clear evidence of frequent and varied vocal and violin portamento use, clear links in portamento use between early-recorded singing and violin playing, and consistency between early-recorded portamenti and written sources from Schubert’s time. To understand why portamento was lost, I examined the wider phenomenon of style change in the 20th century and found that both recording technology and general 20th-century aesthetic changes encouraged “cleanness” and “repeatability” in music, thereby eradicating spontaneous and unique expressive devices like portamento. Finally, I researched innate emotional responses to music and portamento’s importance as an engaging communicative tool, and undertook my own artistic experimentation in early-19th-century music, collaborating with and surveying leading vocal and string 19th-century HIP practitioners to explore ways of making portamento expressive and relevant to modern musical practice and appreciation.

Chapter 4: Appendix 4.2

Mathematical representations of portamento curves

Technical Definitions:

Rate of change: the slope of the graph or the slope of the tangent to a curve if the graph is curved
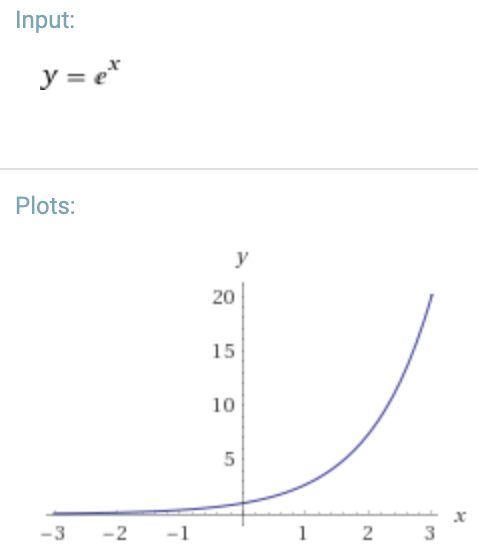
Exponential: graphs in the form y = ae^bx
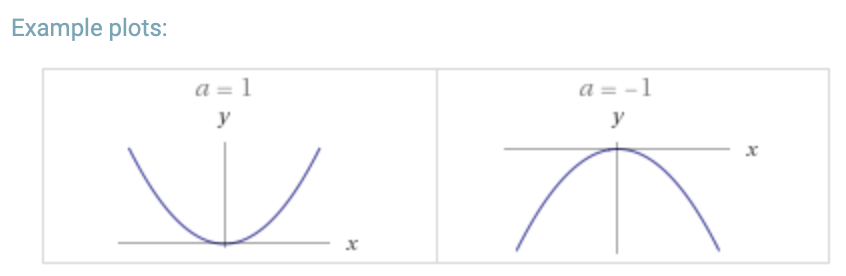
Polynomial: graphs in the form y = ax² = bx + c
Negative/Positive graph: the dominant term in the graph’s equation is negative (N.B. this does not mean that the rate of change is increasing or decreasing)
Growth/Decay: how the rate of change of an exponential differs as x increases (as the graph goes to the right)

Linear:

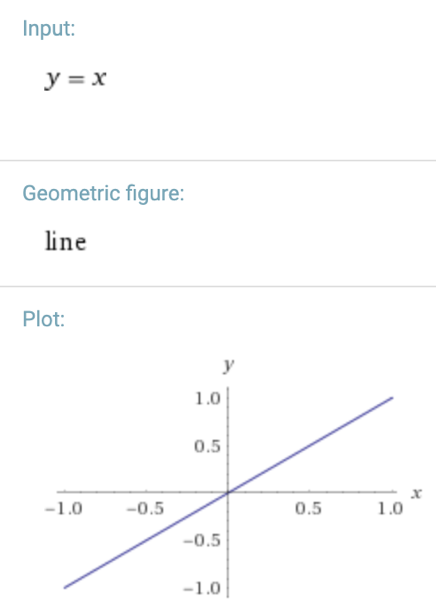
Negative linear: the graph is increasing1

Technical definition: constant rate of change

Visually: a straight line increasing

Equivalent portamento type: usually fast ascending slide with no slowing or quickening of pitch change between notes

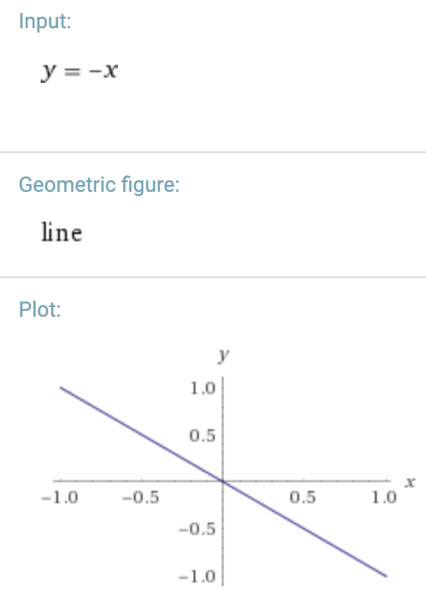
Positive linear: the graph is decreasing2

Technical definition: constant rate of change

Visually: a straight line decreasing

Equivalent portamento type: usually fast descending slide with no slowing or quickening of pitch change between notes

Exponential:

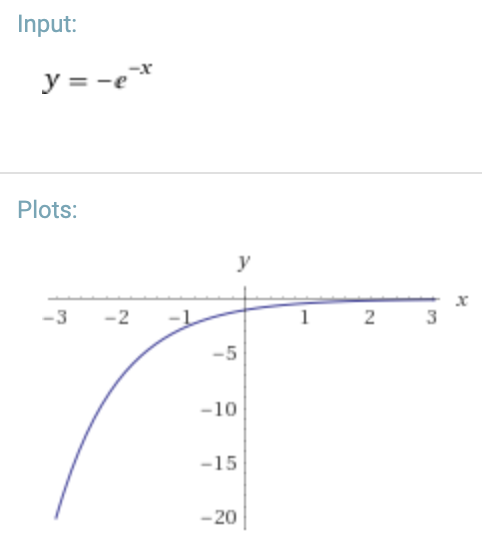
Technical name: negative exponential decay

Visually: increasing pitch, with the rate of change initially steep then decaying to a shallow rate of change3

Equivalent portamento type: ascending slide which starts fast and then slows as it approaches destination note

Technical name: positive exponential growth

Visually: increasing pitch, with the rate of change initially shallow then growing and becoming very steep4

Equivalent portamento type: ascending slide which starts slow and then quickens as it approaches destination note

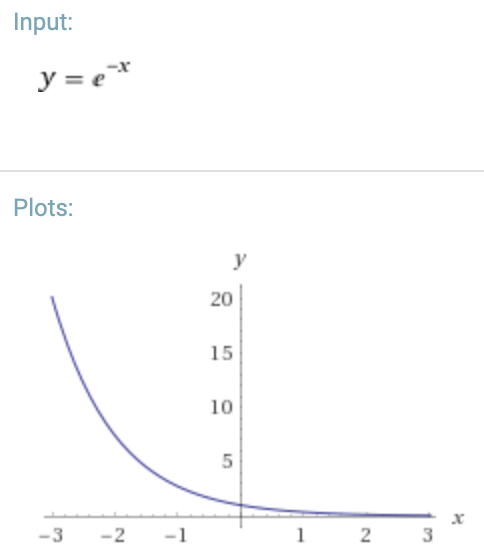
Technical name: positive exponential decay

Visually: decreasing pitch, with the rate of change initially steep by decaying until it is shallow5

Equivalent portamento type: descending slide which starts fast and then slows as it approaches destination note

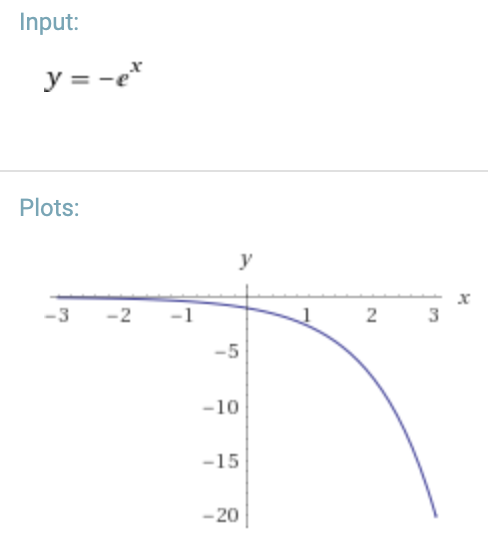
Technical name: negative exponential growth

Visually: decreasing pitch with the rate of change initially shallow then growing until it is very steep6

Equivalent portamento type: descending slide which starts slow and then quickens as it approaches destination note

Parabolic/Quadratic Equation:

Technical definition: Equation in the form y = ax² = bx + c

Visually: initially increasing/decreasing steeply, with the rate of change becoming shallower until it is flat, then decreasing/increasing (opposite of previous mention) at a slow rate of change with the rate of change becoming steeper7

Equivalent portamento type: ascending or descending slide which has a basically constant rate of change of pitch and then slows as it approaches destination note. N.B. this type of graph is not usually relevant for most portamento curves, as parabolas can drastically vary in shape depending on the variant of equation, which makes them difficult to match to the different portamento curves. Exponential graphs tend to fit portamento curves much more accurately.

- Next page -

Tip

Tip