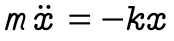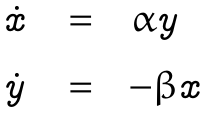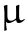Coordinate change
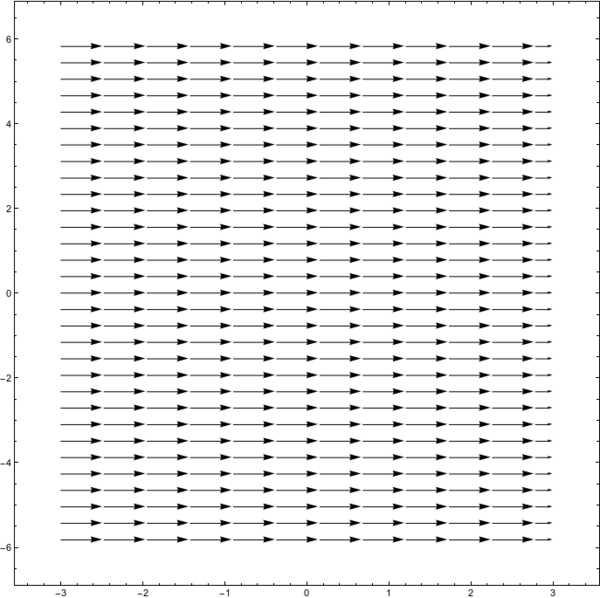
The phase flow of the harmonic oscillator can also be reformulated in a slightly differently. On each radius from the origin, the vector field pushes a point with a constant velocity along a circle. So, we could also say, that the vector field of the harmonic oscillator is a constant on a circle. While, the flow does not "push" in a direction orthogonal to the circle, it does not produce changes in the radius (or amplitude) of the oscillator.
It seems therefore almost natural to reformulate the above equations (in a Cartesian space) in polar coordinates, phase and radius, i.e. an equivalent coordinate space that can highlight the perspective above. We can reformulate the basic harmonic oscillator system as:
The second equation is usually omitted (as clearly it is not so interesting), leaving us with a very concise formulation of oscillatory phenomena. Also, for this reason, as it is done in context of the study of synchronisation phenomena, it is admissible to concentrate on just the differential equation for the phase.
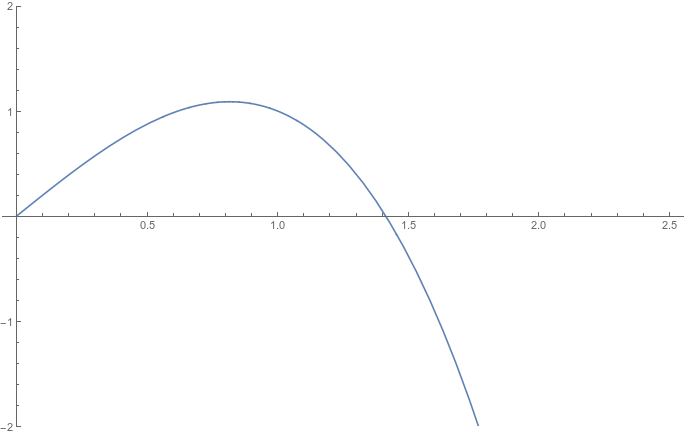
For completeness, note that from the perspective of this coordinate system, also the phase space looks differently (see the figure on the right, the x-axis corresponds to the phase and the y-axis to the radius coordinates). We see a constant of magnitude equal to the frequency of the harmonic oscillator flow directed towards growing values of the phase.